• 이 포스팅은 Andrew Ng 교수님의 Machine Learning 강의를 정리했습니다.

비용 함수(Cost Function)

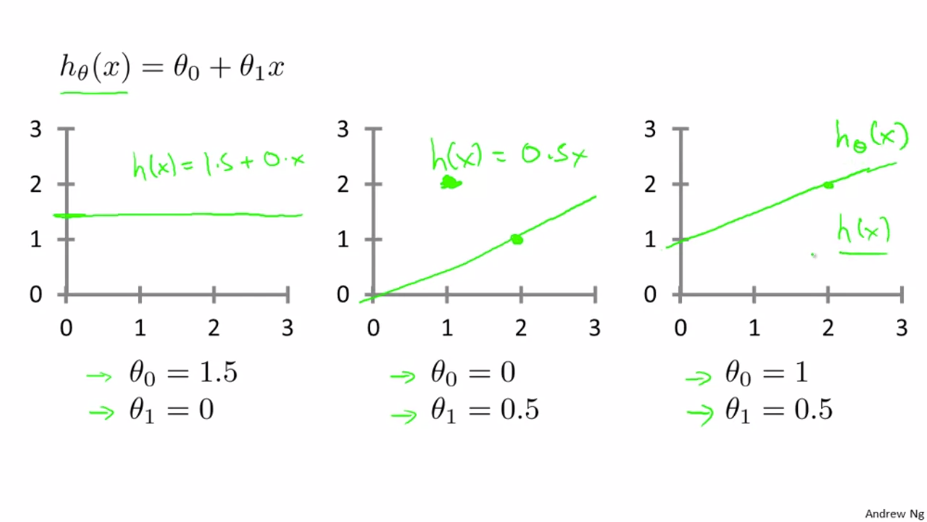
가설함수 h를 구성하는 $\theta _{0}$ 와 $\theta _{1}$은 모형의 파라메터를 나타냅니다. 비용 함수를 사용하면 주어진 데이터에 가장 가까운 일차함수 그래프를 알아 낼 수 있습니다.

선형회귀에서는 $\theta _{0}$과 $\theta _{1}$의 값들을 이용해 다음과 같은 일차함수를 구해, 자료와 얼마나 잘 일치하는지를 봅니다. 이때 비용함수를 사용하면 주어진 데이터에 가장 가까운 일차함수 그래프를 알아낼 수 있습니다.

그러면 어떻게 $\theta _{0}$ 와 $\theta _{1}$가 데이터와 얼마나 잘 일치하는지 알 수 있을까요?

훈련집합의 예시에서 실제로 집이 어떤 가격에 팔리는지 알 수 있습니다. 우리는 θ0 와 θ1의 값을 선택해서 x값이 주어진다면 y값을 예측할 수 있습니다. 주어진 데이터에서 h(x)와 y간의 차이 즉, h(x) - y 를 최소화가 되게 해줄 것입니다. 이 뺀 값을 제곱을 해주고(음수 일 수 있기 때문에) 훈련집합의 크기인 m 까지의 합계를 구합니다. 그리고 이것의 평균값을 구합니다. 식으로 나타내면 이렇습니다.

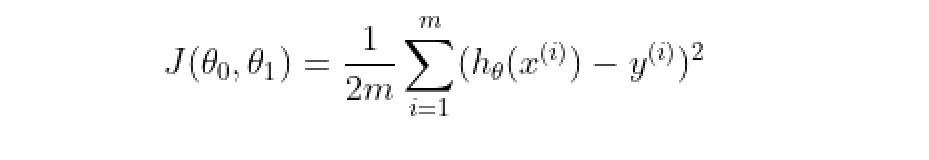
이 J 함수가 비용함수(Cost Function) 입니다. 이 함수는 제곱 오차 함수(Squared error function) 또는 평균 제곱 오차(Mean squared error;MSE) 라고 합니다.

이 함수는 합리적인 선택이며 대부분의 회귀 문제에서 잘 작동합니다.

Cost Function - Intuition I

$\theta _{0}$ 의 값을 0으로 하여 가설 함수 h를 간소화 합니다.

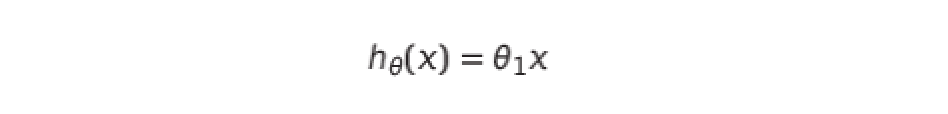
다음과 같은 (0, 0)을 지나는 일차함수를 만들 수 있습니다. 이 간소환 된 가설 함수 h는 비용 함수 개념을 이해하는데 도움을 줍니다.

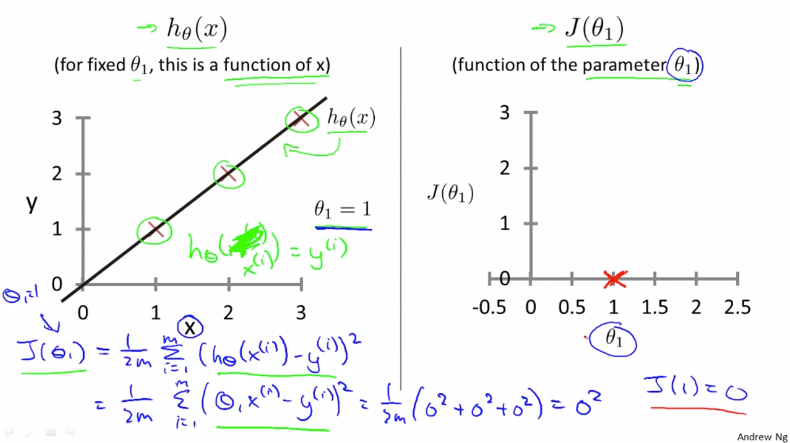
(1, 1), (2, 2), (3, 3) 세가지 점으로 이루어진 훈련집합이 있다고 가정합니다. 비용 함수를 계산해 봅니다.

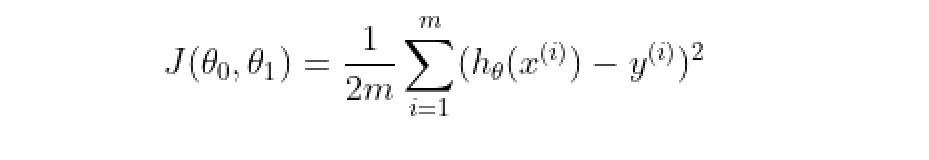
오차의 제곱, 즉 h(x) - y 의 값을 구하면 세가지 점 모두 0이 나오게 됩니다. 그러므로 J($\theta _{1}$) = 0 이라는 비용 함수를 얻을 수 있습니다. 여기서 θ1 = 1 이므로 J(1) = 0 이 됩니다.

이 비용 함수를 그래프에 나타내면 오른쪽 그래프와 같습니다.

다음으로는 θ1 = 0.5 일 경우 입니다.

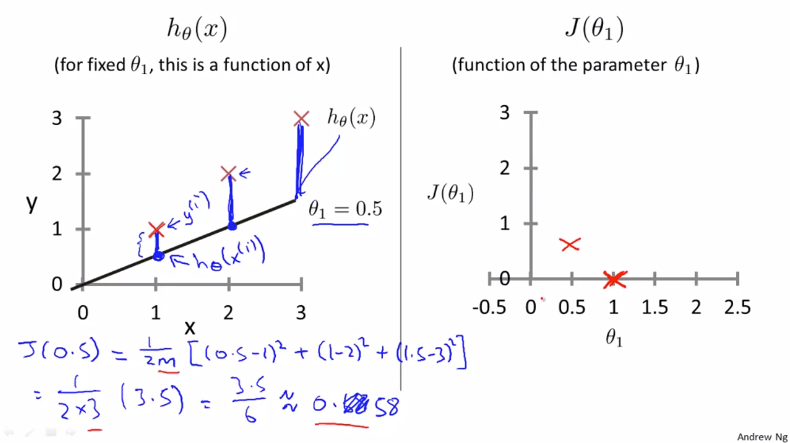
위와 같은 방법으로 오차의 제곱을 계산하게 되면 J(0.5) ≒ 0.58 가 나옵니다. 이 값을 오른쪽 그래프에 추가해줍니다.

이러한 방식으로 θ1에 여러 값에 대한 오차 함수의 값을 이용해 그래프를 그리면 아래 보이는 그래프와 같이 포물선을 그리게 됩니다.

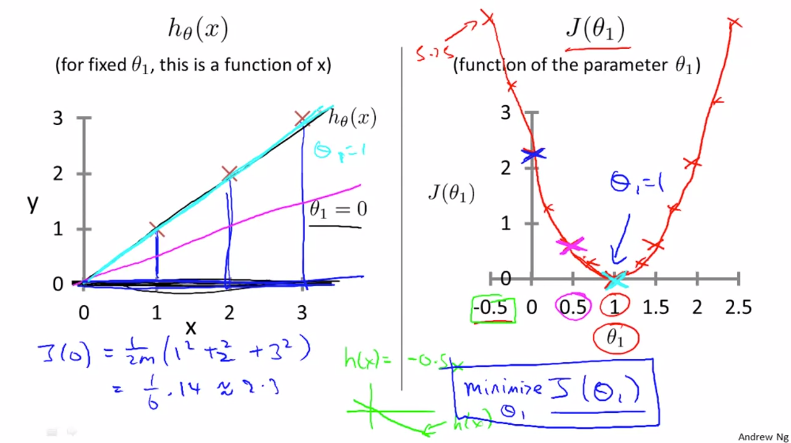
우리의 목표는 J($\theta _{0}$) 값이 최소값이 되는 것입니다. 위 포물선을 보면 J(1) 일때 가장 최소값을 가지게 됩니다. 즉, $\theta _{1}$ 이 1인 직선입니다. 이 직선이 자료와 잘 맞는 다는 것도 확인 할 수 있습니다. 그렇기 때문에 J($\theta _{1}$) 을 최소화한 값이 자료에 잘 맞는 다는 결론을 내릴 수 있습니다.

Cost Function - Intuition II

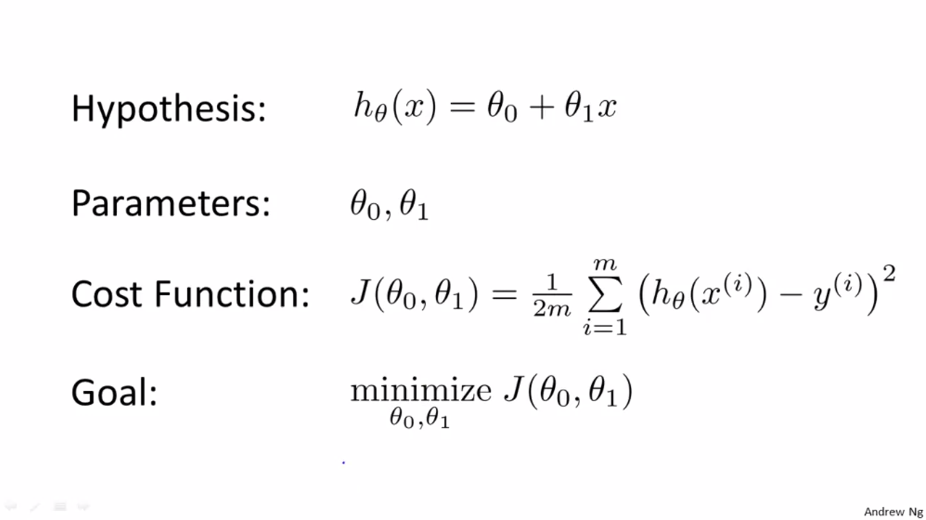
$\theta _{0}$와 $\theta _{1}$이 모두 있는 가설함수를 살펴봅니다.

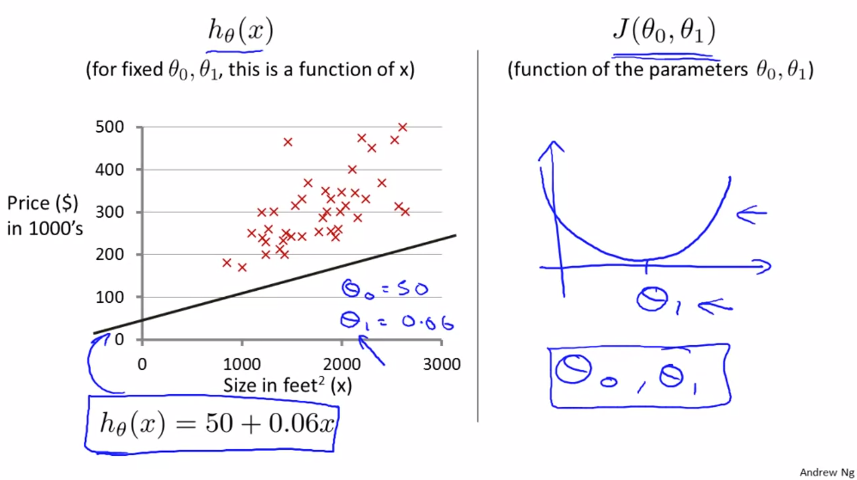
Intuition I 에서는 $\theta _{1}$ 만 사용해 계산했었습니다. 이제 우리는 $\theta _{0}$ 도 사용할 것입니다. 비용 함수를 그려보면 오목한 형태의 그래프를 얻을 수 있습니다.

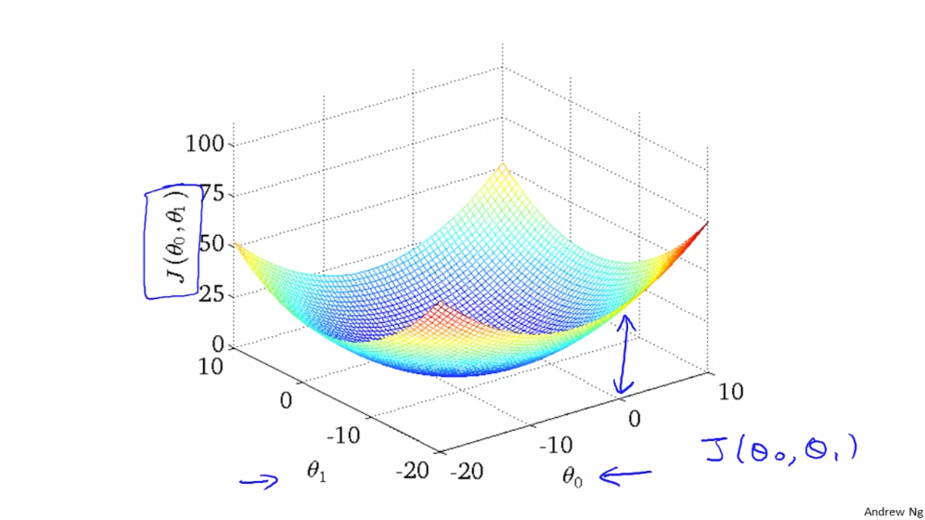
이 그래프는 $\theta _{0}$, $\theta _{1}$, J(θ0, θ1) 를 나타내는 3차원 그래프 입니다. 이 3차원 그래프 대신에 등고선 그래프를 사용하겠습니다.

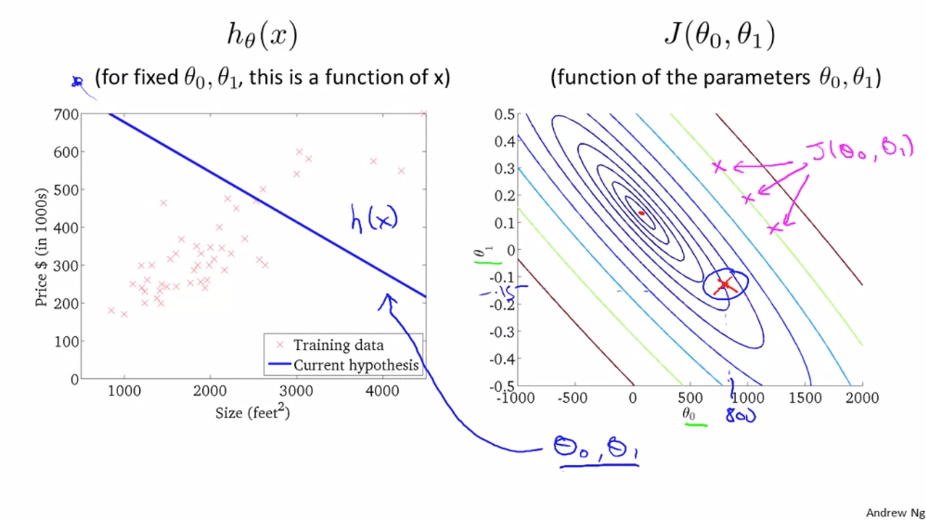
위 그림의 오른쪽 그래프를 보면 $\theta _{0}$ 의 값은 약 -0.15이고 $\theta _{1}$의 값은 800인 점을 확인해봅니다. 이를 이용해 그린 가설 함수 h(x) 는 데이터와 잘 맞지 않는 그래프인 것을 확인 할 수 있습니다.

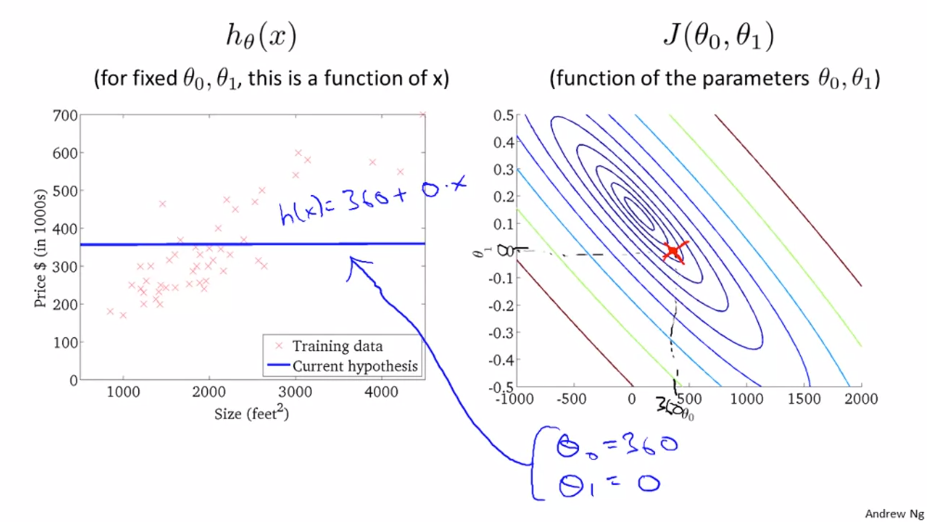
위의 그래프는 $\theta _{0}$의 값이 360, $\theta _{1}$의 값은 0을 나타내고 좋은 그래프는 아니라는 것을 확인 할 수 있습니다.

위의 예시는 완벽한 최소값은 아니지만 최소값에 가깝고 데이터와 비슷한 형태를 나타내고 있습니다. 그래서 결론적으로 비용 함수의 최소값과 비슷할 수록 더 좋은 가설이라는 것을 알 수 있습니다.