[Coursera][Muchine Learning] Gradient Descent 경사 하강법
- 이 포스팅은 Andrew Ng 교수님의 Machine Learning 강의를 정리했습니다.
경사 하강법(Gradient Descent)

경사 하강법은 비용 함수 J의 최소값을 구하는 알고리즘입니다. 이 알고리즘은 기계 학습의 모든 곳에서 실제로 사용되고 있습니다.
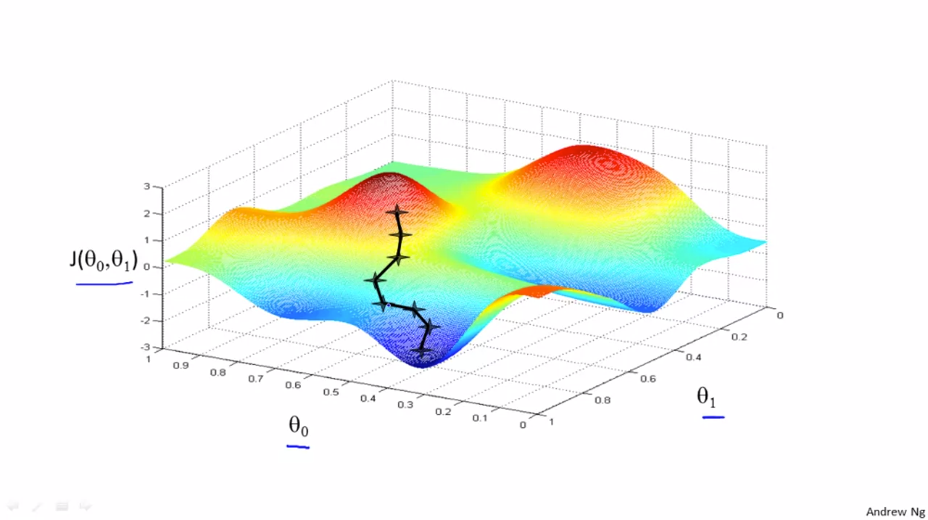
$\theta _{0}$과 $\theta _{1}$ 2가지 파라메터를 사용한 그래프를 사용합니다. 우리는 가장 먼저 θ0과 θ1의 초기값을 추측해야 됩니다.
일반적으로는 초기값을
- $ \theta _{0} = {0}$
- $ \theta _{1} = {0}$
으로 설정합니다. 이제 경사 하강법에서 값을 조금씩 바꾸며 최소의 비용 함수를 찾아냅니다.
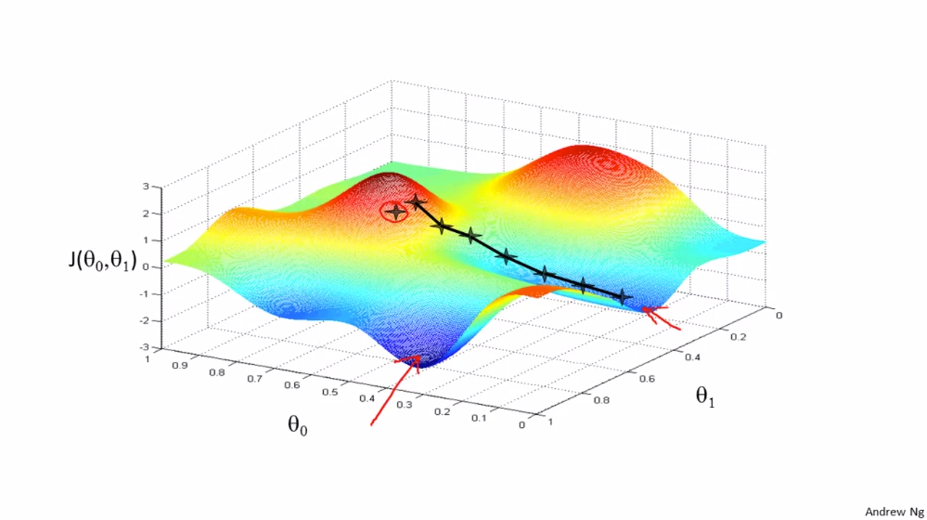
$\theta _{0}$과 $\theta _{1}$을 다른 값으로 초기화 한다면 다른 최적의 결과가 도출 될 수 있습니다.

수학적으로 알아봅니다.
-
:= 는 할당받는 것을 의미합니다. (a := b 라면 b의 값을 a에 씌운다 라는 뜻)
-
$ \alpha $(Learning Rate) 는 훈련 비율이라고 합니다. $ \alpha $값이 클수록 움직이는 거리가 증가합니다.
-
$ \frac{\partial }{\partial \theta _{j}}J(\theta _{0}, \theta _{1} ) $ 는 미분계수입니다.
비용 함수는 $\theta _{0}$과 $\theta _{1}$ 2가지 변수에 의해 영향을 받는데 오른쪽 식과 같이 대입을 하게 되면 $\theta _{1}$ 에 값을 대입할 때 이미 변화된 $\theta _{0}$ 의 영향을 받으므로 왼쪽 식처럼 대입해줘야 합니다.
Gradient Descent Intuition
하나의 파라미터 $ \theta _{1} $ 를 가지고 함수를 최소화한 $ J(\theta _{1}) $ 을 사용합니다.
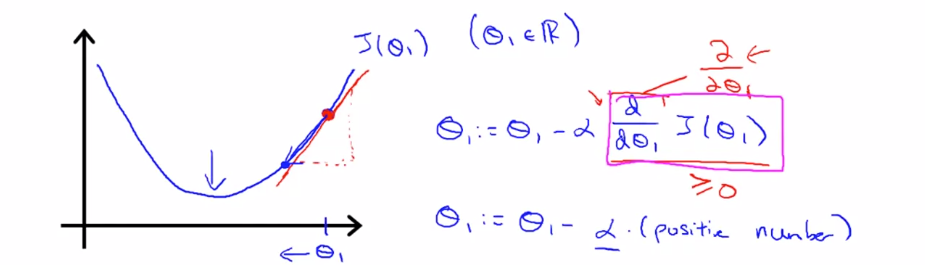
$ \theta _{1} $ 에서의 기울기는 그 점의 탄젠트(Tangent) 값으로 구할 수 있고 그것이 바로 미분계수입니다. 여기서 기울기는 양수이므로 $ \alpha $ 의 값이 양수라는 것 또한 알 수 있습니다. $ \theta _{1} $ 은 이제 $ \alpha $ 에 기울기(양수값)을 곱한 값이 됩니다. 이런식으로 $ \theta _{1} $ 은 최소값으로 이동하게 됩니다.
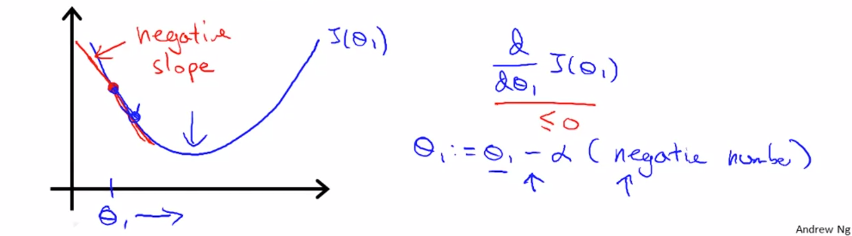
이번엔 $ \theta _{1} $ 를 그래프의 왼쪽으로 초기화 해봅니다. 이때의 기울기는 음수값을 가지게 됩니다. $ \theta _{1} $ 은 $ \alpha $ 값에 음수값(기울기) 를 곱한 값이 되므로 오른쪽으로 이동합니다. 이렇게 계속해서 최소값과 가까운 쪽으로 이동하게 됩니다. 이것이 경사 하강법입니다.
이제 $ \alpha $ 에 대해 알아봅니다.
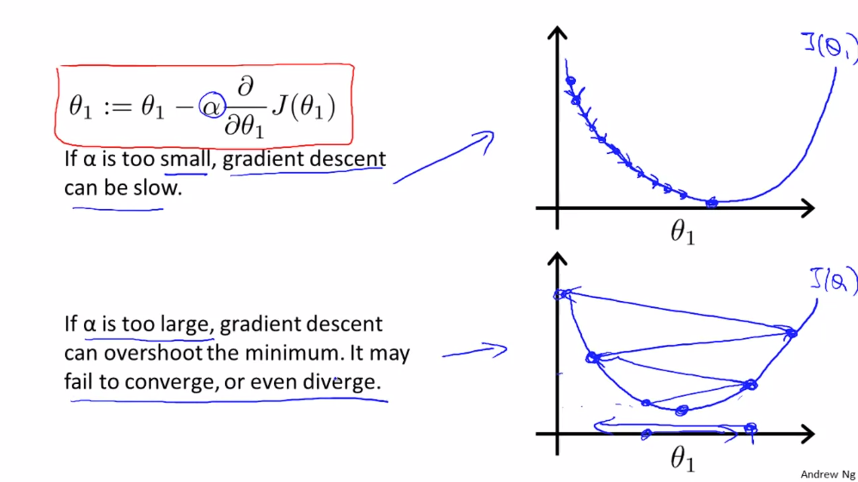
$ \alpha $ 의 값이 너무 작다면 최소값으로 도달하는데에 많은 이동이 필요하게 되고 그만큼 많은 시간이 걸리게 됩니다. 반대로 $ \alpha $ 의 값이 너무 크다면 최소값에 수렴하지 못하거나 발산하게 됩니다.
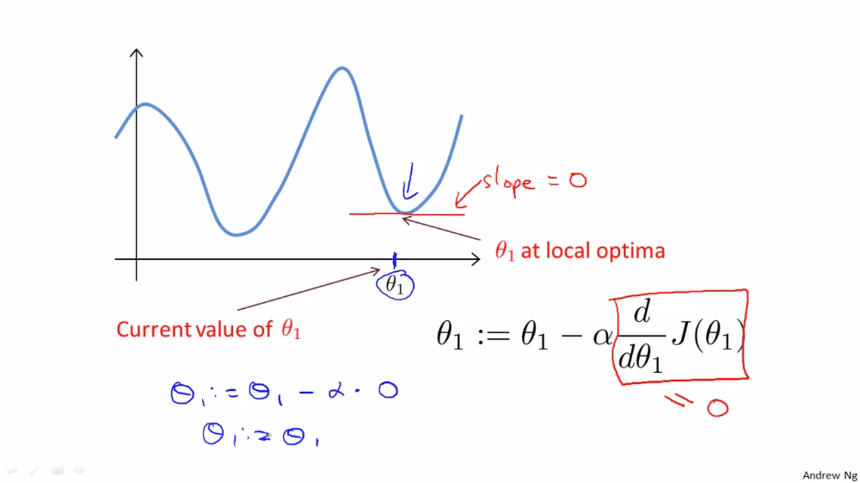
$ \theta _{1} $ 이 최소값(기울기 0)이라면 $ \theta _{1} = \theta _{1} $ 로 아무런 영향을 끼치지 않고 유지됩니다.
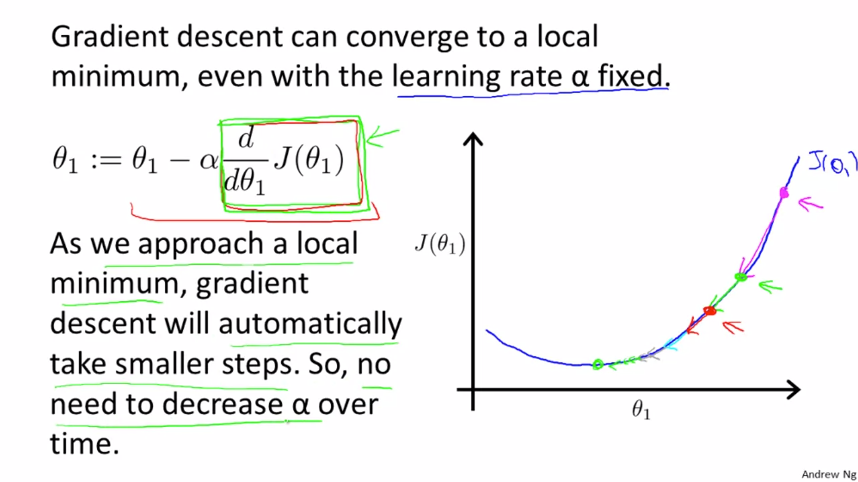
만약 $ \alpha $ 가 고정되어 있어도 문제없습니다. 최소값에 가까워질수록 미분계수는 0에 가까워지기 때문입니다.
Gradient Descent For Linear Regression
경사 하강법을 선현 회귀에 적용합니다.

경사 하강업을 사용해 비용 함수(Cost Function)를 최소화 시킬 것입니다. 경사 하강법을 적용하기 위해 미분 계수를 사용해야합니다.
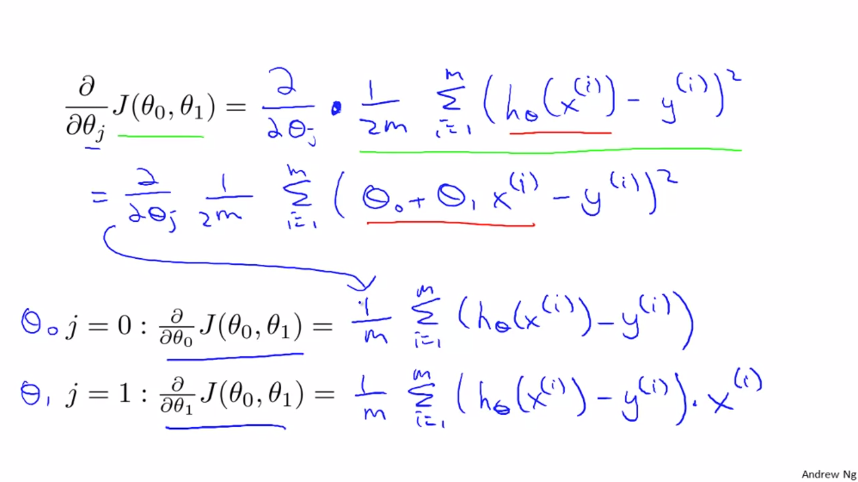
$ \theta _{0} $과 $ \theta _{1} $ 두 가지 경우가 있기 때문에 각각 함수가 나옵니다.

경사 하강법 알고리즘에 적용합니다. 여기서 중요한 점은 $ \theta _{0} $와 $ \theta _{1} $ 를 동시에 구하는 것입니다.
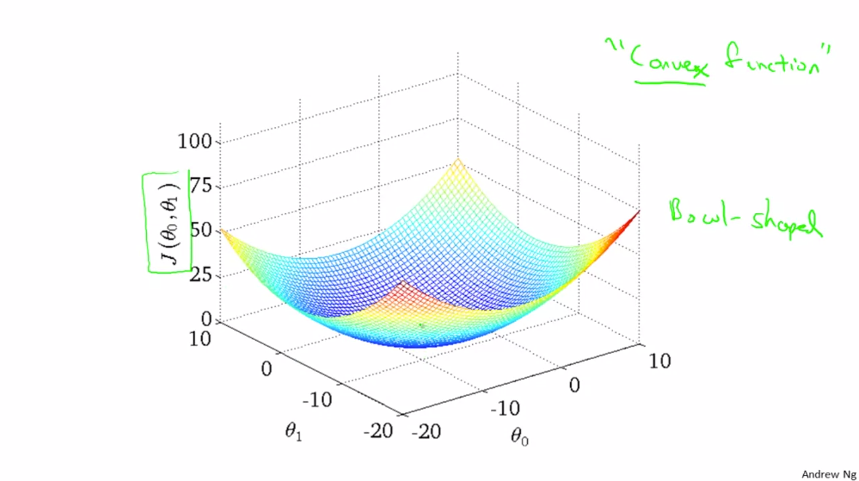
선형 회귀의 비용함수는 항상 볼록 함수 모양이 됩니다. 이는 지역적 최소값이 없고 전역적 최소값만 가지고 있습니다.
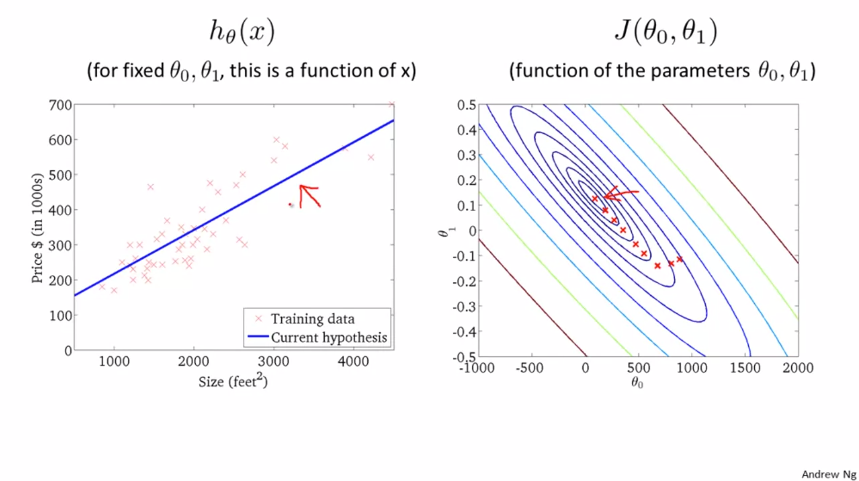
이전에 했던 주택 가격 데이터입니다. 전역적 최소값만 존재하기 때문에 경사 하강 알고리즘을 적용하면 결국 최소값에 도달하게 됩니다.

이 알고리즘은 다른 이름은 집단 기울기 하강(Batch Gradient Descent) 라고도 부릅니다. 집단 기울기 하강은 모든 훈련 데이터를 나타내는 의미입니다.