• 이 포스팅은 Andrew Ng 교수님의 Machine Learning 강의를 정리했습니다.

Matrices and vectors

이부분은 기본 수학적 개념이기 때문에 간단하게만 훑고 지나갑니다.

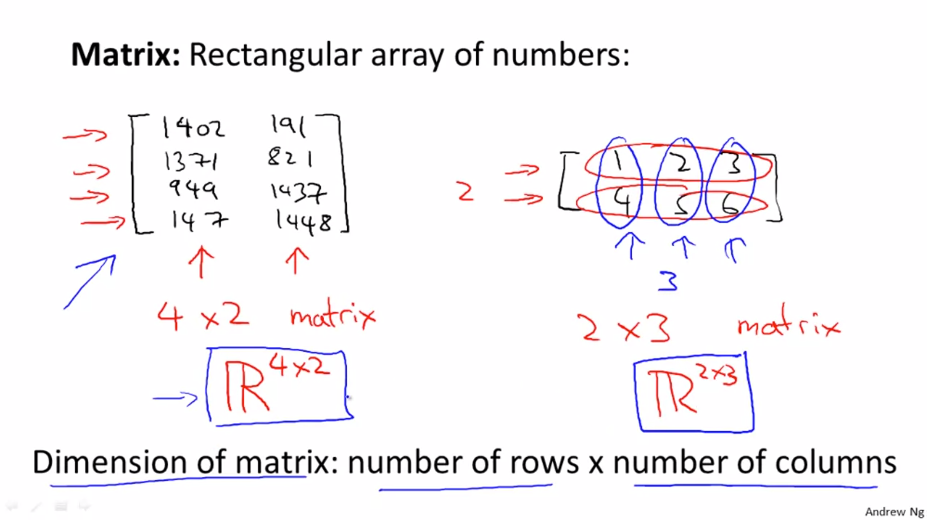
행렬이란 각 괄호안에 나열된 숫자들의 배열을 말합니다.

왼쪽을 4 x 2 행렬(Matrix) 이고 오른쪽은 2 x 3 행렬입니다.

행렬 내의 특정 원소를 지칭하기 위해서는 $ A_{ij} $ 에서 i(행), j(열) 을 지정해 주면 됩니다.

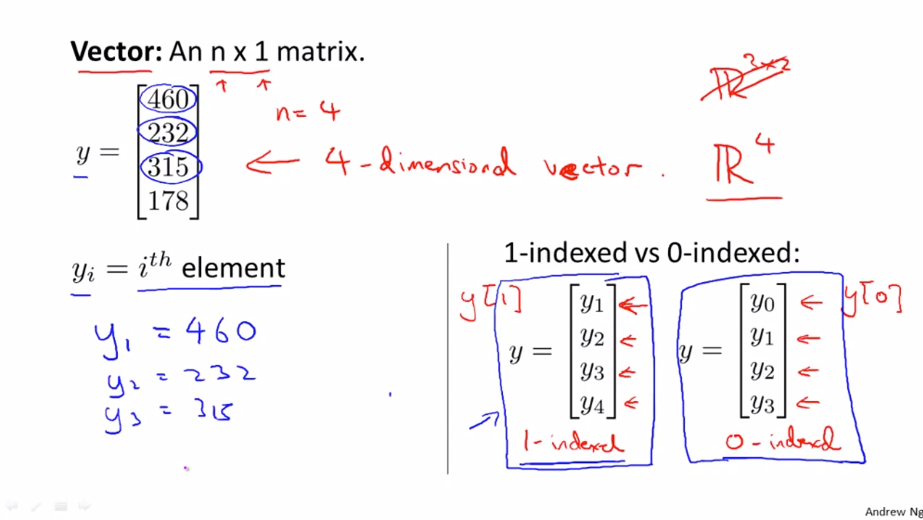
벡터(Vector)는 한 개의 열만을 가진 행렬입니다. 즉, n x 1 행렬을 벡터라고 부릅니다. 벡터는 1부터 시작하는 1-Indexed vector 와 0부터 시작하는 0-Indexed vector 가 있습니다. 실제 수학에서는 1-Indexed vector, 기계학습에서는 0-Indexed vector를 주로 사용합니다. 이 강의에서는 1-Indexed vector를 사용합니다.

Matrix Addition

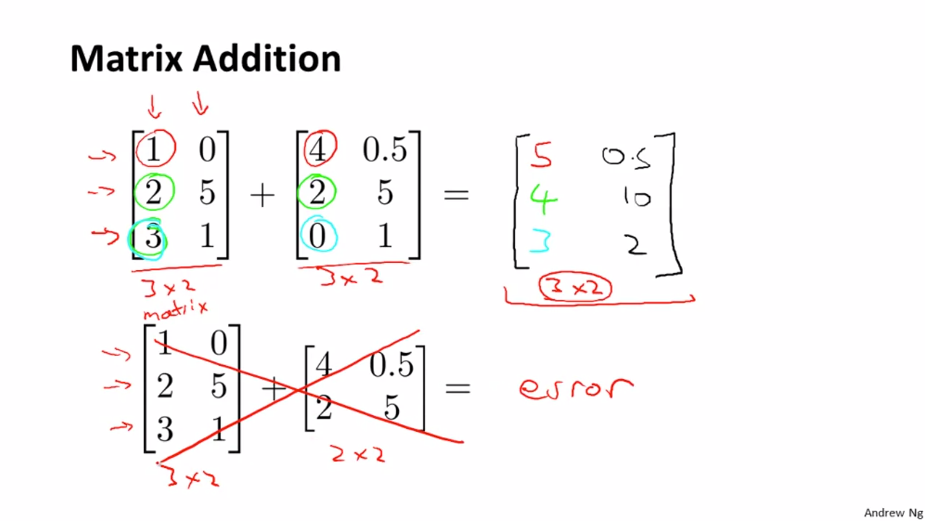
행렬의 덧셈은 같은 차원의 행렬들만 더할 수 있습니다. 같은 차원의 행렬은 같은 위치에 있는 것을 더하면 됩니다. 뺄셈도 같은 방법으로 진행합니다.

Scalar Multiplication

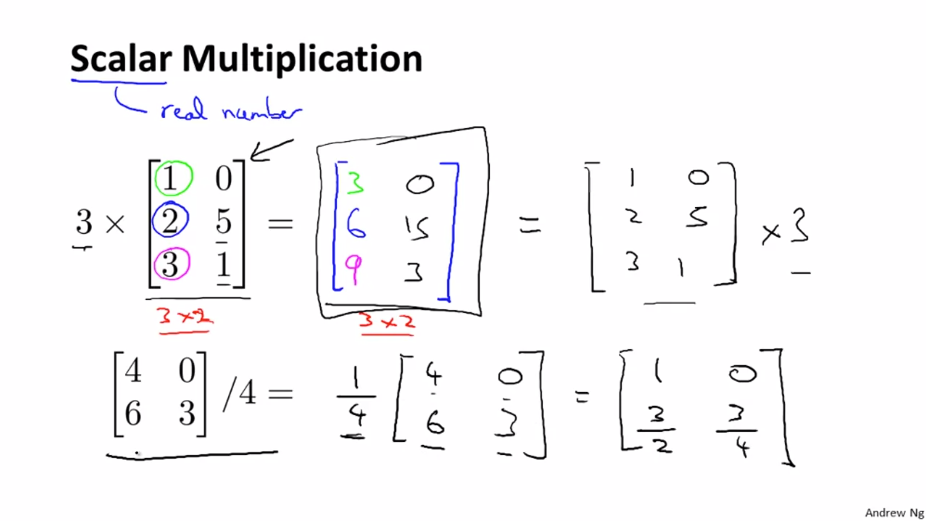
스칼라(Scalar)는 실수라는 뜻입니다. 그러므로 행렬에 실수를 곱하는 것입니다. 실수를 각 행렬의 요소에 곱합니다. 그 결과는 같은 차원의 행렬이 나오게됩니다.

나눗셈도 같은 방법으로 진행합니다.

Matrix Vector Multiplication

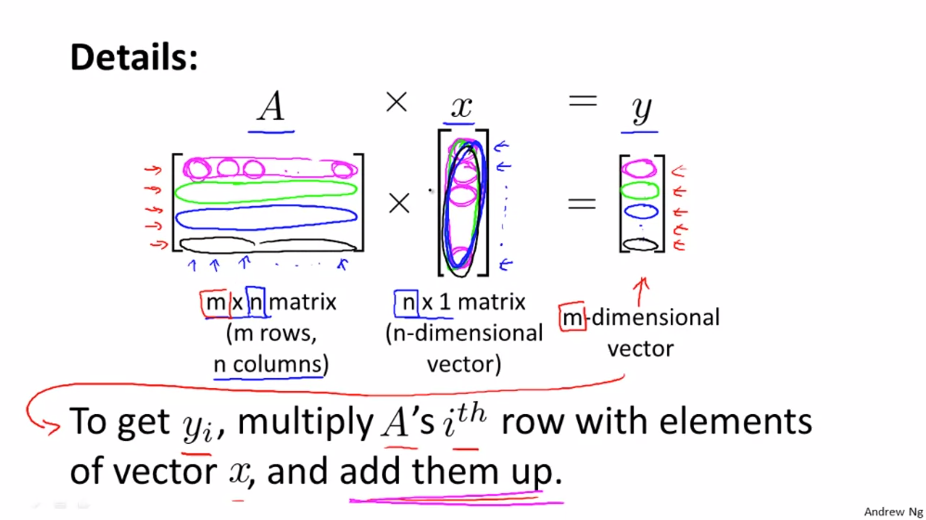
행렬과 벡터의 곱셉입니다. m x n 행렬과 n x 1 행렬(n 차원 벡터) 을 곱하면 m x 1 행렬(m 차원 벡터) 를 얻을 수 있습니다.

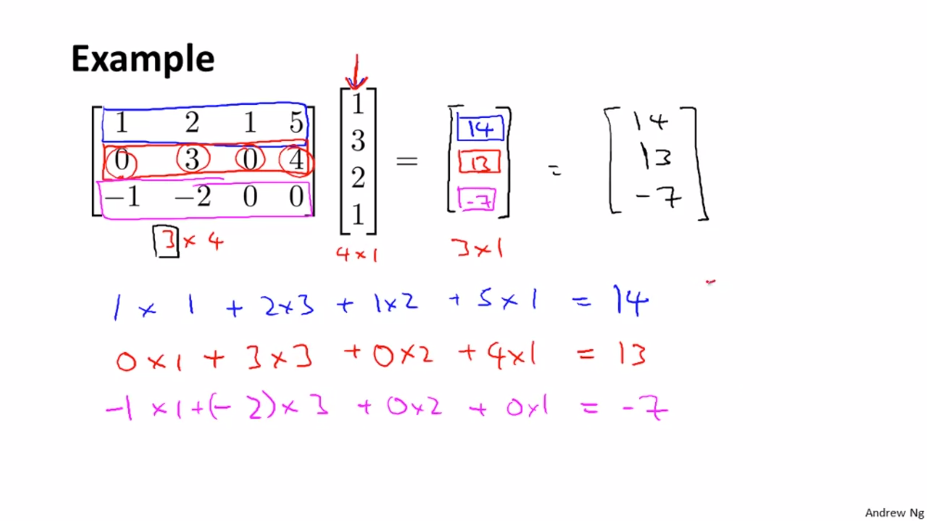
즉 다음과 같이 3 x 4 행렬과 4 x 1 행렬의 곱셈 결과는 3 x 1 행렬(3 차원 벡터)가 나오게 됩니다.

Matrix Matrix Multiplication

행렬과 행렬의 곱셈입니다. 예제를 살펴보면 벡터로 나누어서 곱셈을 진행한 후 합쳐주는 방식을 사용하고 있습니다.

m x n 행렬과 n x o 행렬의 곱은 m x o 행렬의 결과를 얻을 수 있습니다.

Matrix Multiplication Properties

실수나 스칼라의 곱셈은 교환법칙이 성립합니다. 하지만 행렬의 곱셈에는 교환법칙이 적용되지 않습니다.

행렬의 곱은 순서를 바꾸면 차원이 변합니다. 예를들어 A (m x n 행렬) 와 B (n x m 행렬)을 곱하면 A x B 는 m x m 행렬이 되고 B x A 는 n x n 행렬이 됩니다.

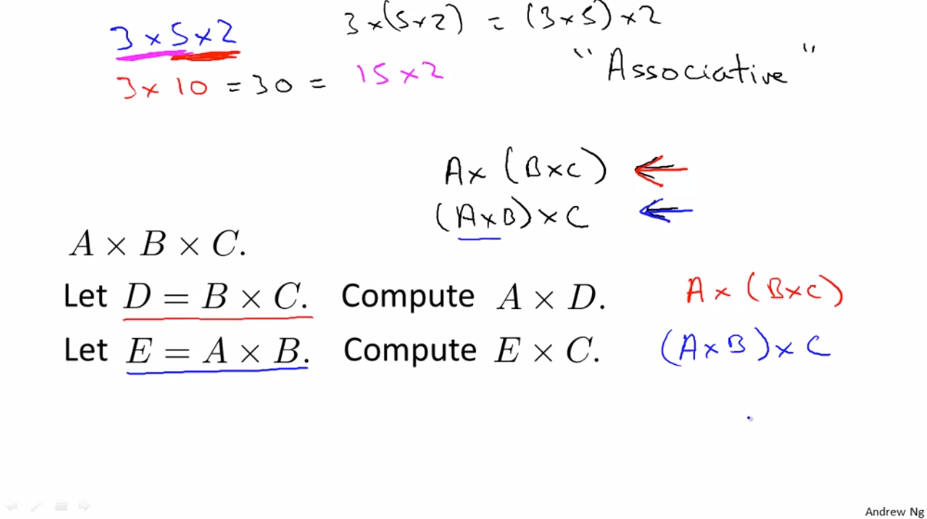
다음은 결합 법칙입니다. 실수나 스칼라와 같이 행렬의 곱셈은 결합 법칙이 적용됩니다.

Identity Matrix

대각선 성분들이 1이고 나머지는 0인 행렬은 항등 행렬이라고 부르고 n x n 항등 행렬은 $ I _{n \times n} $ 로 표시합니다.

항등 행렬은 어떠한 행렬에 앞이나 뒤에 곱해도 자기자신이 나온다는 것입니다.

Inverse and Transpose

역행렬 (Inverse)

실수에서 1은 항등원 역할을 합니다. 실수는 각각 역수를 가지고 있습니다. 실수와 그 역수를 곱하면 항등원 1이 됩니다. 하지만 모든 실수가 역수를 가지고 있지 않습니다. ($ {0}^{-1} $ 는 정의 되지 않습니다.)

행렬을 살펴봅니다. A는 n x n 행렬이라고 정의합니다. 행렬 A는 정방 행렬(행과 열의 수가 같은 행렬)입니다. 행렬은 정방 행렬만이 역행렬을 가질 수 있습니다. 그렇기 때문에 행렬 A는 역행렬을 가질 수 있고 $ A^{-1} $ 으로 표현합니다.

행렬 A와 역행렬을 곱하게 되면 항등 행렬이 됩니다. 정방 행렬은 모두 역행렬을 가지지만 실수에서와 같이 정방 행렬의 모든 값이 0이면 역행렬을 가지지 않고 이러한 행렬을 Sigular matrix 또는 Degenerate matrix 라고 합니다.

전치 행렬(Transpose)

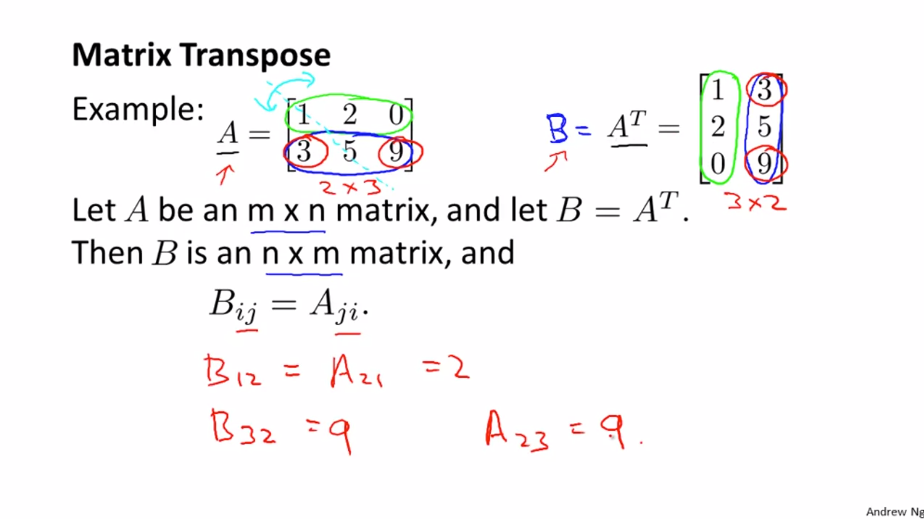
전치 행렬은 행과 열의 차원을 서로 바꾸는 것입니다. 즉, n x m A행렬의 전치 행렬 B는 m x n 행렬이 되고 $ A^{T} $ 로 표현합니다.

그러므로 $ A _{ij} = B _{ji} $ 가 성립합니다.