• 이 포스팅은 Andrew Ng 교수님의 Machine Learning 강의를 정리했습니다.

Multiple Features

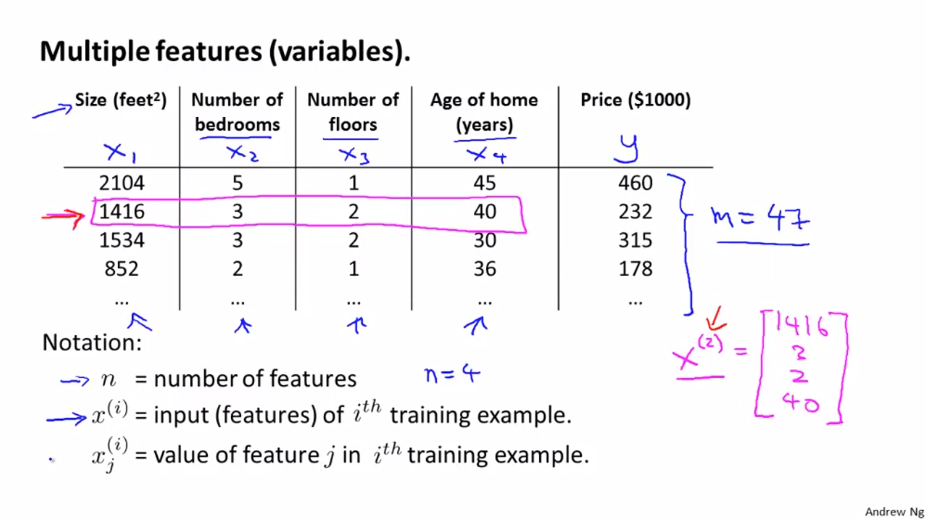
앞서 배운 선형 회귀에서는 집의 크기로 집의 가격을 결정하는 단일 요소(Feature) 를 알아봤습니다. 하지만 ‘침실의 개수’, ‘집의 연식’ 과 같은 정보를 알고 있다면 집의 가격을 결정하는데에 더 많은 요소(Feature)를 갖고 있는 것이 됩니다.

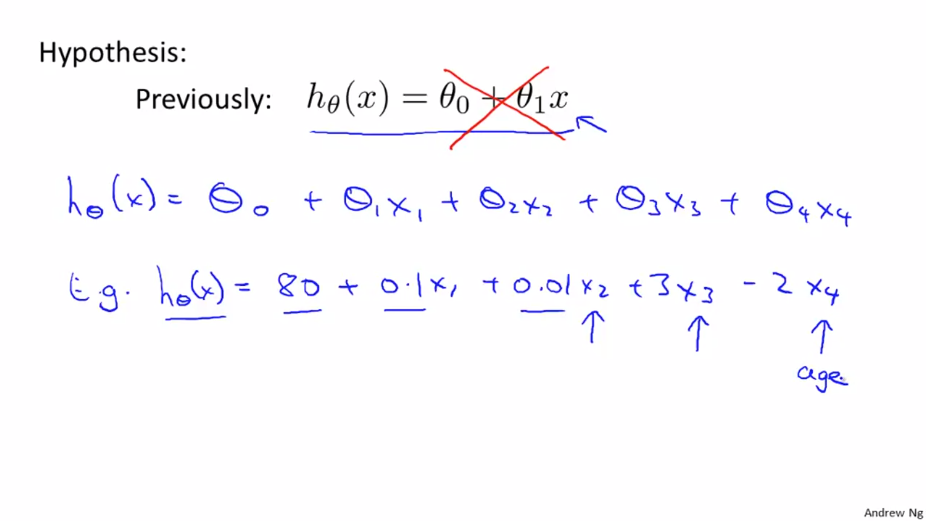
우리는 이제 여러개의 요소(Feature) 를 가지고 있기 때문에 식이 단순하게 표현되지 않습니다.

Feature 벡터 $ x $와 Parameter 벡터 $ \theta $ 가 있습니다. 가설함수 h는 transpose한 Parameter 벡터와 Feature 벡터의 곱이 됩니다.

$$ h _\theta(x) = \begin{bmatrix} \theta _{0} \theta _{1} … \theta _{n} \end{bmatrix} \begin{bmatrix} x _{0} \\ x _{1} \\ … \\ x _{n}\end{bmatrix} = \theta^{T}x $$

Gradient Descent for Multiple Variables

앞서 여러 요소(Feature) 를 이용한 선형 회귀에 대해 살펴봤습니다. 이번에는 추론의 파라미터를 어떻게 지정하고 어떻게 다변량 선형 회귀(Multivariate Linear Regression) 에 경사 하강법을 적용하는지 알아봅니다.

두개 이상의 요소를 가지고 있다고 가정합니다. 우리는 $ \theta _{0} $, $ \theta _{1} $, $ \theta _{2} $ 에 대응되는 세가지 update 규칙을 적용하면 오른쪽과 같은 식을 얻을 수 있습니다.

Feature Scaling

여러개의 feature 가 있고 서로 다른 feature 라도 범위가 비슷하다면, Gradient descent 는 더 빠르게 수렴할 수 있습니다.

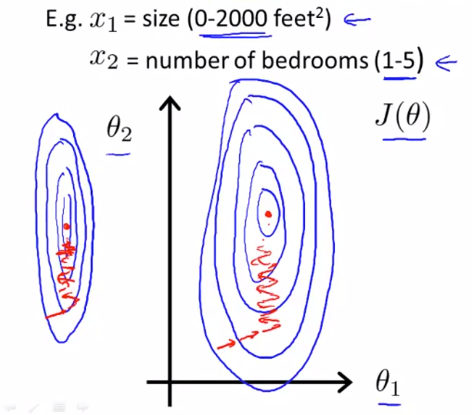
다음 그래프를 살펴봅니다. $ x _{1} $ 은 집의 크기이고 범위는 0 에서 2000사이의 값을 가집니다. $ x _{2} $ 는 침실의 수로 1에서 5사이의 값을 가집니다. 이를 이용해 cost function $ J(\theta) $ 를 그리게 되면 길고 얇은 타원 모양의 그래프를 얻을 수 있습니다. 만약 이 cost function에 gradient descent 를 적용한다면 최소값까지 오랜 시간이 걸릴겁니다.

이럴때 유용한 방법이 feature 를 조절(scale) 하는 것입니다.

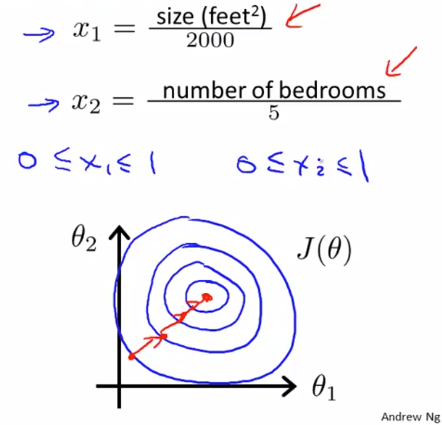
$ x _{1} $ 를 2000으로 나눈 값과 $ x _{2} $를 5로 나눈 값으로 cost function를 구하면 원에 가까운 타원 모양의 그래프를 구할 수 있습니다. 이러한 비용함수에 gradient descent 를 적용하면 좀 더 정확한 방향으로 최소값을 찾는 것을 볼 수 있습니다.

feature scaling 을 할 때, feature 가 대략 -1에서 1 사이의 범위에 있기를 원하지만 이 범위에 근사하다면 이것은 중요하지 않습니다. 하지만 만약 feature 의 범위가 아주 크거나(-100 에서 100 범위) 아주 작다면 ( -0.00001에서 0.00001 사이) 의 값을 가진다면 feature 를 조절해야 합니다.

Mean normalization

feature scaling을 할 때 mean normalization 를 할 수 있습니다. feature 의 값에 해당 feature 의 평균을 빼고 데이터의 범위나 표준편차로 나누어 주는 것입니다. feature scaling 은 너무 정확할 필요는 없습니다. gradient descent가 더 빨라지는 것이 목적이기 때문입니다.

Learning Rate

다음 그래프에서 x축은 gradient descent의 반복 횟수입니다. y축은 반복한 후의 cost function $ J(\theta) $ 입니다. gradient descent 가 잘 돌아간다면 $ J(\theta) $ 는 매 반복마다 감소해야 합니다. 위의 그래프에서 400번 반복 후에는 거의 수렴하는 것으로 보입니다. 수렴에 필요한 반복 횟수는 경우에 따라 다양합니다.

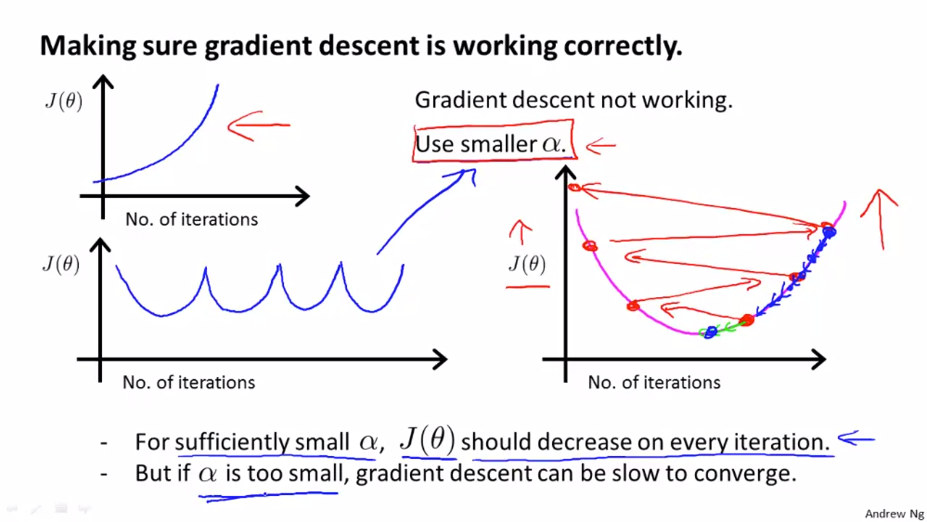
위의 왼쪽에 있는 그래프는 gradient descent 가 제대로 동학하지 않을 경우입니다. 이러한 상황에서는 더 작은 $ \alpha $ (learning late) 를 사용해야합니다. 보통은 더 작은 $ \alpha $ 를 사용하게 되면 문제가 해결 됩니다. 하지만 $ \alpha $ 가 너무 작으면 오래걸리는 문제가 발생 할 수 있습니다. 그렇기 때문에 여러번의 시험을 통해 적당한 $ \alpha $ 를 찾는 과정이 필요합니다.

Features and Polynomial Regression

feature를 간단하게 선택하는 방법과 적절한 feature 의 선택으로 강력한 학습 알고리즘을 만드는 방법에 대해 알아봅니다.

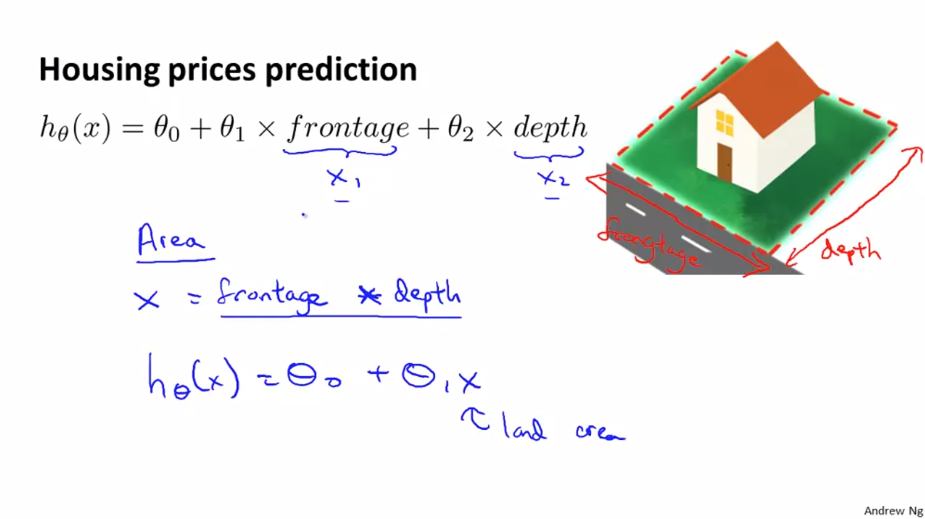
집값 예측에서 2개의 feature로 집의 너비 frontage 와 집의 세로길이 depth 가 주어집니다. 선형 회귀 모델을 만들때 frontage를 $ x _{1} $ depth를 $ x _{2} $ 로 사용 할 수 있습니다. 하지만 우리는 이러한 feature 를 사용하지 않고 frontage x depth 로 구할 수 있는 집의 넓이를 나타내는 새로운 feature를 만들어 사용할 수 있습니다.

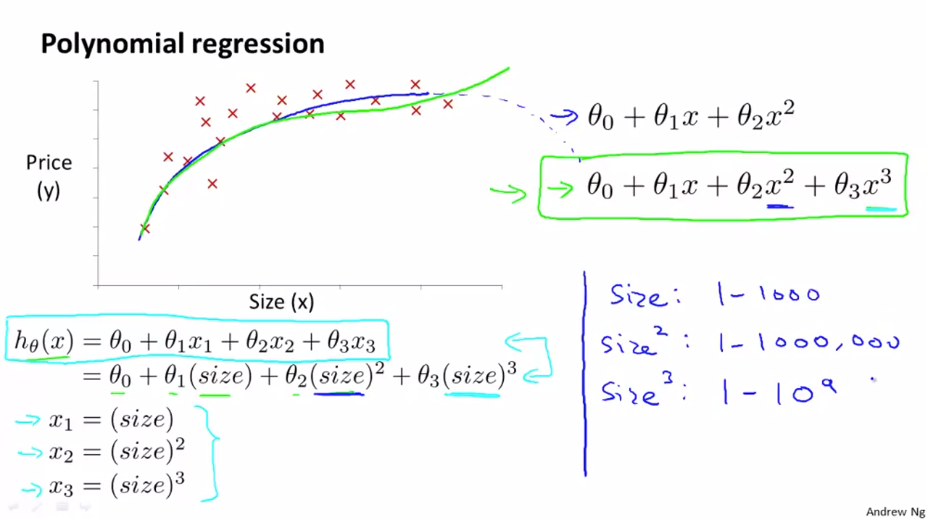
다음과 같은 data set 은 직선으로 표현하기 어렵습니다. 그래서 2차 함수 모델(파란선)로 표현 할 수 있습니다. 하지만 2차 함수는 결국 하강하기 때문에 적합하지 않습니다. 그래서 2차 함수 대신에 3차 함수(초록선)를 사용할 수 있습니다.

3차식 모델로 표현하기 위해서 $ x _{1} $ 을 집의 크기, $ x _{2} $ 를 집의 크기의 제곱, $ x _{3} $ 는 집의 크기의 세제곱으로 치환합니다. 하지만 이와 같이 feature 를 사용하게 되면 feature scaling 의 적용이 중요해집니다. 3가지의 feature 가 매우 다른 값의 범위를 가지게 되기 때문입니다.

위에서 소개한 3차식 모델외에도 다른 방법이 있습니다.

다른 예로 제곱근 함수를 사용하는 것 입니다. 여러개의 서로 다른 feature 가 있을 때는 어떤 feature를 사용해야하는지 혼라스러운 상황이 있을 수 있습니다. 후에, 자동으로 어떤 feature 를 사용하는지 골라주는 알고리즘에 대해서 배울 것 입니다.