• 이 포스팅은 Andrew Ng 교수님의 Machine Learning 강의를 정리했습니다.

Cost Function and Backpropagation

Cost Function

분류 문제에 신경망을 적용하는데에 초점을 맞춰 진행합니다.

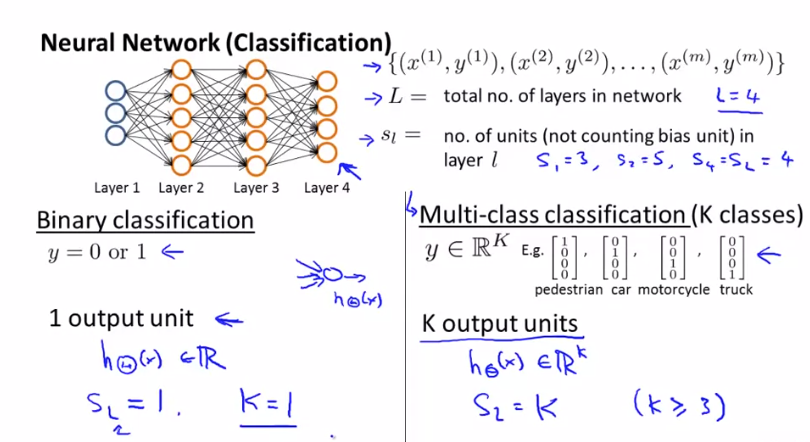
  • L은 네트워크의 총 Layer 수를 나타냅니다.

  • $ s _{l} $ 은 뉴런의 수를 나타냅니다.

  • K 는 Output Layer 수를 나타냅니다.

이진 분류(Binary Classification)와 다중 클래스 분류(Multi-class Classification) 문제로 나누어 보겠습니다. 이진 분류는 1개의 Output unit을 가지고 다중 클래스 분류는 K개의 분리된 class가 있으므로 K개의 Output unit을 가집니다.

신경망에 대한 비용 함수(Cost Function)를 봅시다.

신경망에 사용하는 비용 함수는 로지스틱 회귀(Logistic Regression)의 비용 함수가 일반화 된 것입니다.

Back Propagation Algorithm

이전에 배운 비용 함수를 최소화하는 역전파(Back Propagation) 알고리즘을 살펴봅니다.

$ J(\Theta) $ 를 최소화 하기 위해 Gradient descent나 다른 최적화 알고리즘을 사용해 매개변수 $ \Theta $를 찾아야합니다.

우리가 해야할 것은 매개변수 $ \Theta $ 를 이용해 $ J(\Theta) $ 를 계산하고 편미분하는 코드를 쓰는 것입니다.

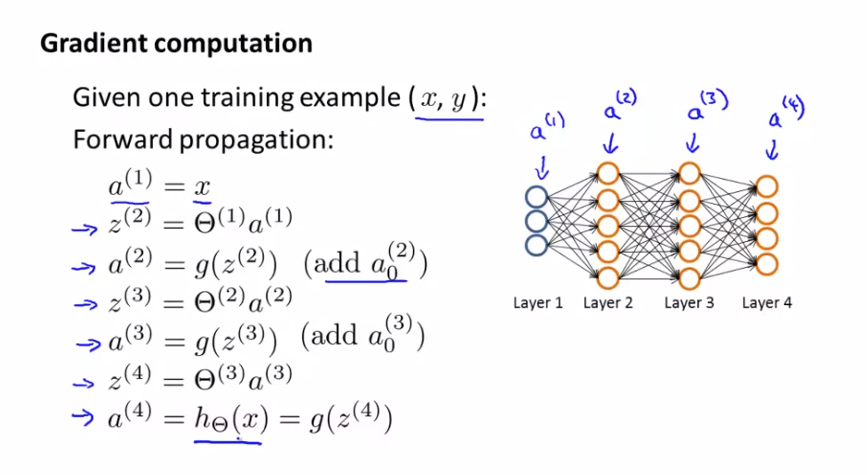
앞서 배운 순전파(Forward propagation) 은 Input Layer 부터 Output Layer 로 진행된다는 것을 배웠습니다. 이와 반대로 역전파(Back propagation)은 Output Layer 에서 시작해 error 값을 이용해 각 Layer 에서 error를 계산합니다.

각 node 의 error는 $ \delta _{j}^{(l)} $ 로 나타냅니다. 위에서 보는것과 같이 Layer 가 4개인 경우 $ \delta _{j}^{(4)} $ 는 계산된 $ a _{j^{(4)}} $ 값고 label의 결과값 y의 차가 됩니다.

$$ \delta _{j}^{(4)} = a _{j^{(4)}} - y _{j} $$

이런 식으로 $ \delta _{j}^{(3)} $ 을 거쳐 $ \delta _{j}^{(2)} $ 까지 거꾸로 계산해 나가기 때문에 역전파 라는 이름을 가지게 됐습니다. 여기서 $ \delta _{j}^{(1)} $ 은 Input Layer 라 오류가 없기 때문에 존재하지 않습니다.

이제 m개 예제로 구성된 훈련세트에서 어떻게 동작하는지 살펴봅니다.

$ \Delta $ 를 모든 l, i, j 에 대해서 0으로 설정하고 이것은 $ J({\Theta}) $ 의 편미분 항을 계산하는데 사용됩니다.

진행과정을 살펴보면 i = 1부터 m 까지 반복하면서 훈련 예제를 학습시킵니다. Input Layer 부터 최종 레이어 L 까지 순방향 전파를 수행한 후 Output Layer 부터 $ \delta $ 를 계산해 역으로 계산합니다.

Back Propagation Intuition

역전파를 더 잘 이해하기 위해 순방향 전파를 자세히 살펴보겠습니다.

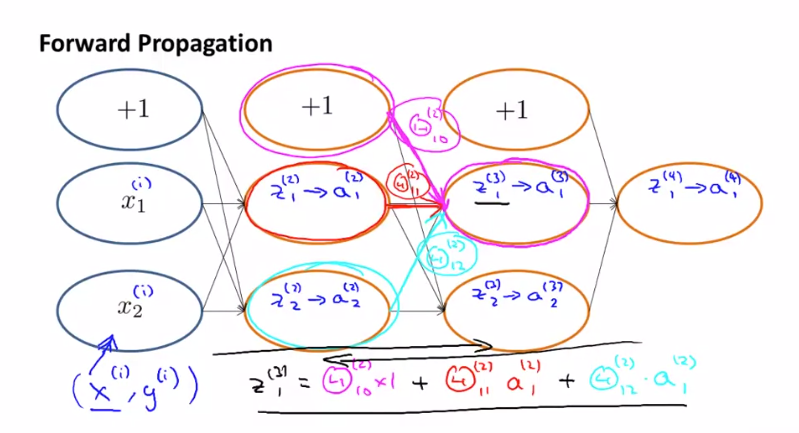
1개의 Input Layer 와 2개의 Hidden Layer, Output Layer 로 이루어진 신경망 입니다. 위의 상황에서 $ z _{1}^{(3)} $ 을 구한다고 하면 $ z _{1}^{(3)} = \Theta _{10}^{(2)} a _{0}^{(2)} + \Theta _{11}^{(2)} a _{1}^{(2)} + \Theta _{12}^{(2)} a _{2}^{(2)} $ 로 구할 수 있습니다. 여기서 $ a _{0}^{(2)} $ 은 bias unit으로 +1을 나타냅니다.

역전파는 순방향 전파 알고리즘을 실행하지만 역방향으로 계산됩니다.

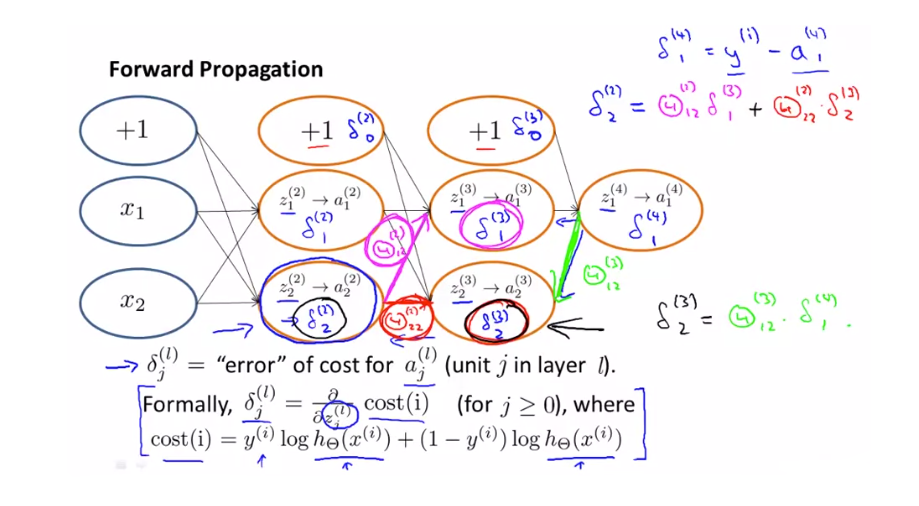
$ \delta _{1}^{(4)} $ 부터 시작해 $ \delta^{(2)} $ 까지 구하게 됩니다. 여기서 $ \delta _{2}{(2)} = \Theta _{12}^{(2)} \delta _{1}^{(3)} + \Theta _{22}^{(2)} \delta _{2}^{(2)} $ 를 구할 수 있습니다.

마찬가지로 $ \delta _{0} $ 은 항상 +1 값을 가집니다.