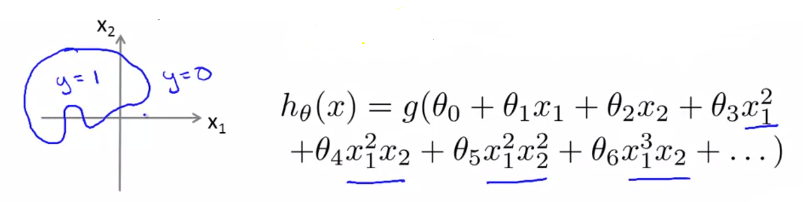• 이 포스팅은 Andrew Ng 교수님의 Machine Learning 강의를 정리했습니다.

분류(Classification)

스팸 이메일 검출, 특정 거래가 사기인지 아닌지, 악성 종양과 영성 종양을 구분하는 문제 등 0 또는 1로 예측하는 것을 분류라고 합니다. 보통 0을 음성 분류라고 하고 1을 양성 분류라고 합니다. 2진분류(binary class) 문제를 먼저 다뤄봅니다.

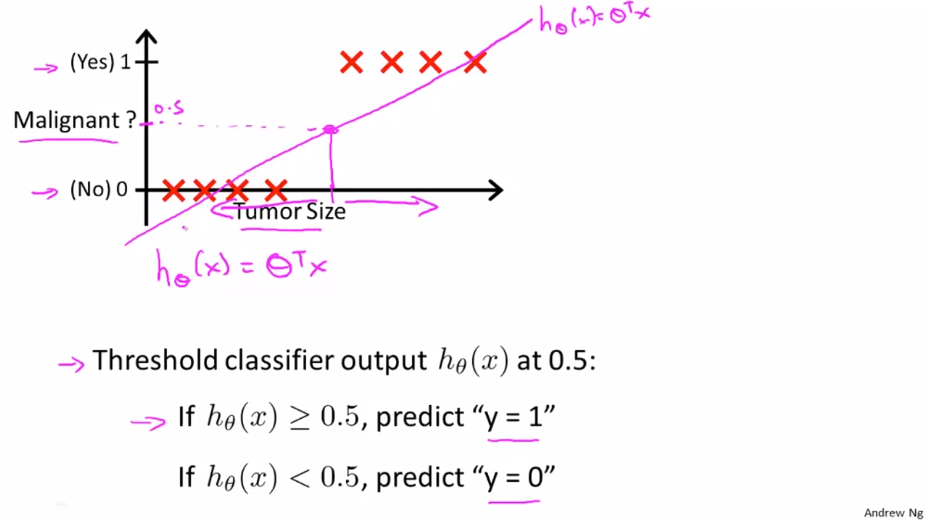
이전에 알아보았던 종양크기 분류에 대한 문제를 살펴봅니다. 주어진 데이터에서 가설 함수 $ h _{\theta}(x) = \theta^{T}x $ 를 구할 수 있습니다. 여기에 임계값 y=0.5 를 설정하여 가설이 0.5보다 크거나 같으면 1, 0.5보다 작을 경우 0으로 예측할 수 있습니다. 이 예시에서는 선형 회귀 모델이 합리적으로 작동하는 것 처럼 보일 수 있습니다. 이번에는 다른 상황을 살펴 봅니다.

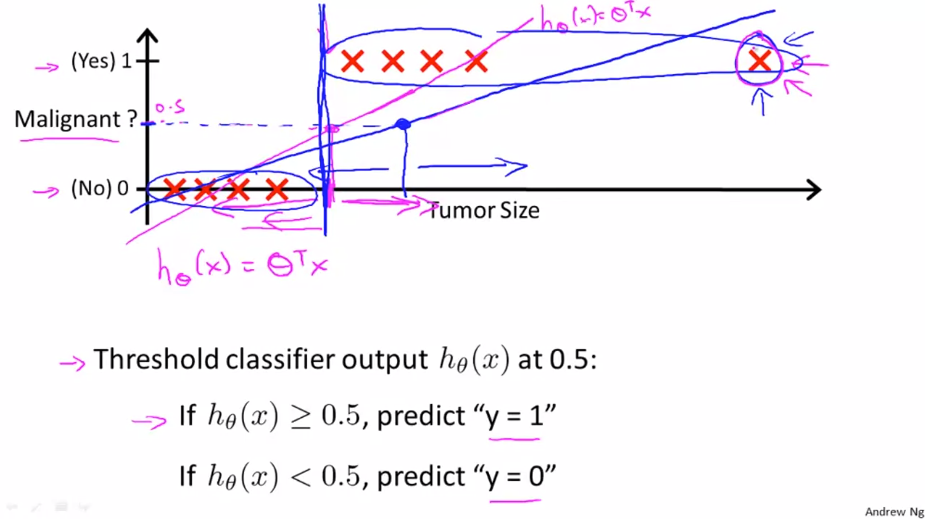
기존 데이터에 수평축을 확장한 후 끝쪽에 학습 데이터를 추가한 경우 입니다. 이 상태로 선형 회귀를 진행해 봅니다. 그리고 임계값을 0.5로 지정 합니다. 학습 데이터를 추가한(파란색) 상태에서는 좋은 결과를 얻지 못하는 것을 볼 수 있습니다.

이러처럼 선형 회귀를 적용하면 운이 좋을 경우 좋은 결과를 얻을 수 있지만 대부분은 잘못된 결과를 얻을 것입니다. 그렇기 때문에 분류 문제에서 대해서는 선형 회귀를 사용하지 않을 것입니다.

또다른 예시로 분류 문제에서 선형 회귀를 사용할 경우 훈련용 데이터 y값이 전부 0이나 1로 설정되어 있어도 가설의 결과값이 1보다 크거나 0보다 작을 수 있습니다.

앞으로의 강의에서 로지스틱 회귀라고 불리는 분류 알고리즘을 공부할 것입니다. 로지스틱 회귀의 결과는 항상 0에서 1사이이며 1보다 크거나 0보다 작은 값을 가질 수 없습니다.

Hypothesis Representation

로지스틱 회귀(Logistic Regression) 모델의 $ h _{\theta}(x) $는 0과 1사이의 범위를 만족해야 합니다.

기존의 선형 회귀 분석을 사용 할 때에 가설 함수 $ h _{\theta}(x) = \theta^{T}x $는 위에서 살펴본 예시와 같이 잘못된 결과를 가져올 수 있기 때문에 적합하지 않습니다. 따라서 로지스틱 회귀는 가설 함수를 $ h _{\theta}(x) = g(\theta^{T}x) $ 로 표현합니다.

여기서 $ g(z) = \frac{1}{1+e^{-z}} $ 이고 이를 적용하면 다음과 같은 식과 그래프를 얻을 수 있습니다.

$$ h _{\theta}(x) = \frac{1}{1+e^{-\theta^{T}x}} $$

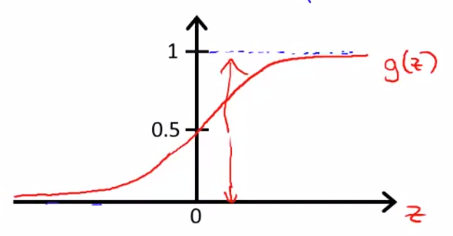
이 그래프는 0과 1의 값만 나타내며 시그모이드 함수 혹은 로지스틱 함수로 불립니다.

주어진 x에 대한 $ h _{\theta}(x) $의 결과값은 y=1 일 확률을 나타냅니다.

종양 분류의 문제라고 생각하고 특정 크기의 종야을 가진 환자가 추가 됐다고 가정해봅니다. 환자들의 특징인 벡터 x를 추가하고 그 결과로 0.7의 값을 얻었습니다.

여기서 이 가설이 말해주는 것은 특징 x를 가진 환자는 악성 종양(y=1)일 확률이 0.7 즉, 70%라는 것이고 양성 종양(y=0)일 확률은 30%라는 것을 알 수 있고 다음과 같이 표현 할 수 있습니다.

Decision Boundary

가설 함수 $ h _{\theta}(x) = \frac{1}{1+e^{-\theta^{T}x}} $ 에서 우리는 결과값이 0.5 이상일때 1, 0.5 미만이면 0의 값을 얻을 수 있습니다.

다음 training set 을 확인해 봅니다.

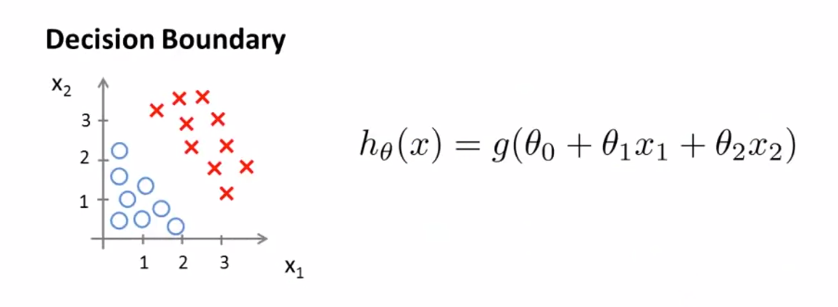
다음 가설 함수에서 $ \theta _{0} = {-3} $, $ \theta _{1} = {1} $, $ \theta _{2} = {1} $ 이라면

$$ {-3} + x _{1} + x _{2} \geq {0} $$

를 얻을 수 있습니다. 이는 $ x _{1} + x _{2} \geq {3} $ 이면 1, 그렇지 않으면 0으로 분류합니다.

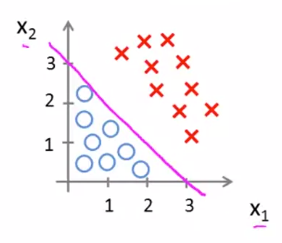
이때의 $ x _{1} + x _{2} = {3} $ 의 방정식이 Decision Boundary 입니다. Decision Boundary는 학습 데이터에 의해 결정되지 않고 $ \theta $ 에 의해 결정됩니다.

조금 더 복잡한 예제로 확인해 봅니다.

우리는 로지스틱 회귀 분석에서 더 높은 차수의 다항식을 사용할 수 있습니다.

다음 함수에서 $ \theta _{0} = {-1} $, $ \theta _{1} = {0} $, $ \theta _{2} = {0} $, $ \theta _{3} = {1} $, $ \theta _{4} = {1} $ 이라면 다음과 같은 식을 얻을 수 있습니다.

$$ {-1} + x _{1}^{2} + x _{2}^{2} \geq {0} $$

여기에서 우리는 다음과 같은 원 모양의 Decision boundary를 얻을 수 있습니다.

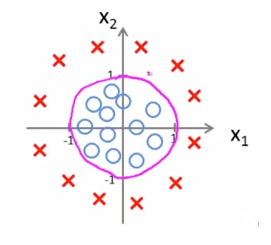
$$ x _{1}^{2} + x _{2}^{2} = {1} $$

이 외에도 더 복잡한 Decision boundary 를 얻을 수 있는 경우도 높은 차수의 다항식으로 얻을 수 있습니다.