• 이 포스팅은 Andrew Ng 교수님의 Machine Learning 강의를 정리했습니다.

Normal Equation

normal equation 은 특정 선형 회귀 문제에서 최적의 파라미터 $ \theta $ 값을 구하는데 효과적인 방법입니다. 지금까지 선형 회귀에서 $ J(\theta) $ 를 최소화 하기 위해 gradient descent 알고리즘을 여러번 반복해 최소값으로 수렴하는 방법을 사용했습니다. 이와는 반대로 normal equation 는 $ \theta $ 의 최적값을 분석적으로 한번에 구합니다.

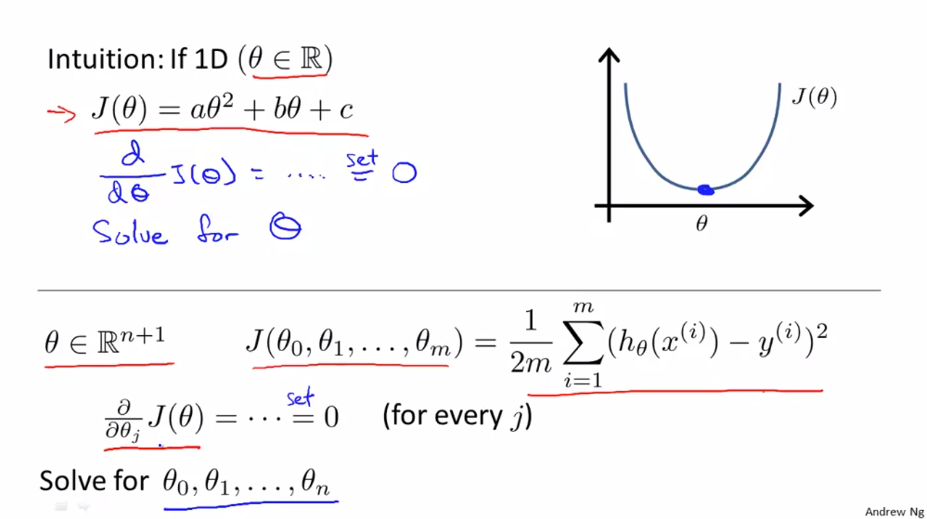
$ \theta $ 가 스칼라 값만 가지고 있다고 가정합니다. 비용 함수 J는 $ \theta $에 대한 2차 함수입니다. 여기서 2차 함수를 최소화 하는 방법은 미분을 하고 미분값이 0이 되는 지점을 찾으면 됩니다. 그러면 이제 $ \theta $ 가 실수가 아닌 (n+1)차원 파라미터 벡터일 경우를 살펴봅니다. 비용 함수 J도 벡터 값($ \theta _{0} $부터 $ \theta _{n} $)에 대한 함수입니다. 이 비용 함수 J 를 최소화 하는 방법은 J를 편미분하는 방법이 있습니다.

m=4 인 training example 을 봅니다.

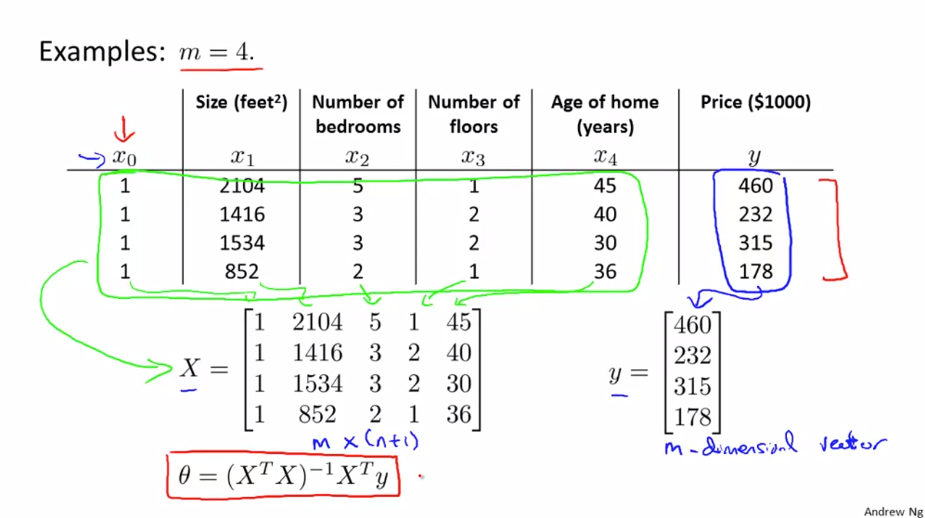
우리가 가장 먼저 해야할 것은 모두 1의 값을 가지는 feature $ x _{0} $ 열을 추가하는 것입니다. 그 다음으로 training data의 모든 feature를 가지는 행렬 X를 만듭니다. 똑같이 예측하려는 값을 가진 벡터 y를 만듭니다. X는 (m x n+1) 차원 행렬이 되었고 y는 m차원 벡터가 됐습니다. 이제 우리가 원하는 값 $ \theta = (X^{T}X)^{-1}X^{T}y $ 를 계산하면 됩니다.

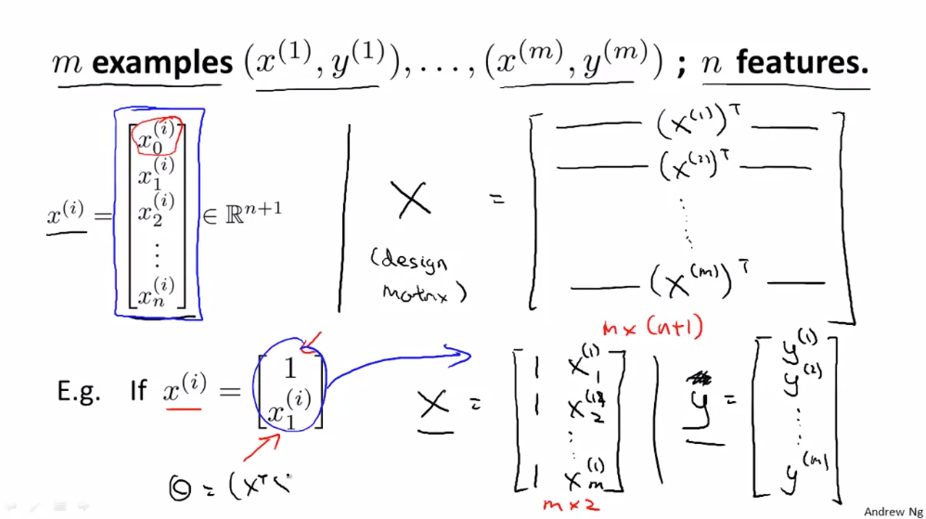
일반적인 경우를 보면 다음과 같습니다.

normal equation 을 사용한다면 feature scaling 이 필요하지 않습니다. 하지만 gradient descent를 사용한다면 feature scaling은 필요합니다.

gradient descent와 normal equation을 비교하면 다음과 같습니다.

gradient descent의 단점은 $ \alpha $(learning rate) 를 정해야 한다는 것입니다. 또 다른 단점은 반복이 많다는 것입니다. 이와 반대로 normal equation은 $ \alpha $(learning rate) 를 정할 필요가 없고 반복도 없습니다.

gradient descent 의 장점은 feature 가 많을 때 효과적 입니다. 반대로 normal equation은 $ \theta $ 를 구하기 위해 $ (X^{T}X)^{-1} $ 를 계산해야 합니다. 이 과정에서 시간이 많이 걸리게 됩니다. 특히 n이 엄청 커지면 normal equation은 훨씬 더 느려집니다. 만약 n=10000이상이라면 gradient descent를 사용하는게 낫습니다.

예를들어 분류(classification) 알고리즘 중에서도 logistic regression 알고리즘 같은 정교한 학습 알고리즘에는 normal equation은 적합하지 않지만 gradient descent는 적합합니다.

Normal Equation Noninvertibility

$ \theta = (X^{T}X)^{-1}X^{T}y $ 를 계산할 때 행렬 $ X^{T}X $의 역행렬을 구할 수 없는 경우가 있습니다. 그 행렬은 비가역행렬(non-invertible matrix), 특이 행렬(singular matrix) 혹은 degenerate matrix 라고 부릅니다. 사실 $ X^{T}X $ 의 역행렬이 없는 경우는 거의 없습니다. Octave 에서는 Pinv()와 Inv() 함수를 사용해 역행렬이 없더라도 $ \theta $ 값을 정확히 계산할 수 있습니다.

$ X^{T}X $가 역행렬이 없는 경우는 대체로 두 가지입니다.

  • 첫번째, 불필요한 feature 를 가지고 있는 경우 입니다. 예를 들어 집 값을 예측하는데 $ x _{1} $ 은 피트 단위의 집의 크기이고 $ x _{2} $는 제곱미터 단위의 집의 크기입니다. 1미터는 약 3.28 피트이므로 $ x _{1} = (3.28)^{2} x _{1} $ 의 선형 관계를 가지게 되고 $ X^{T}X $ 의역행렬이 없다는게 증명이 됩니다. feature 가 서로 관련이 있다면 불필요한 feature 를 제거해야 합니다.

  • 두번째, 많은 feature 를 가지고 학습 알고리즘을 사용 할 때 입니다. training data (m) 보다 feature(n) 이 더 큰경우 (m=10, n=100)라면 벡터 $ \theta $ 는 101차원 (n+1 차원) 이 되고 10개의 training data 로 101개의 파라미터를 표현하려한다면 data가 충분하지 않습니다. 이 때는 feature 를 몇개 제거하거나 regularization을 사용합니다.

하지만 역행렬이 존재하지 않는 경우는 거의 존재하지 않으며 그렇다 하더라고 Octave의 pinv()함수를 사용하면 올바르게 계산할 수 있습니다.