• 이 포스팅은 Andrew Ng 교수님의 Machine Learning 강의를 정리했습니다.

Cost Function

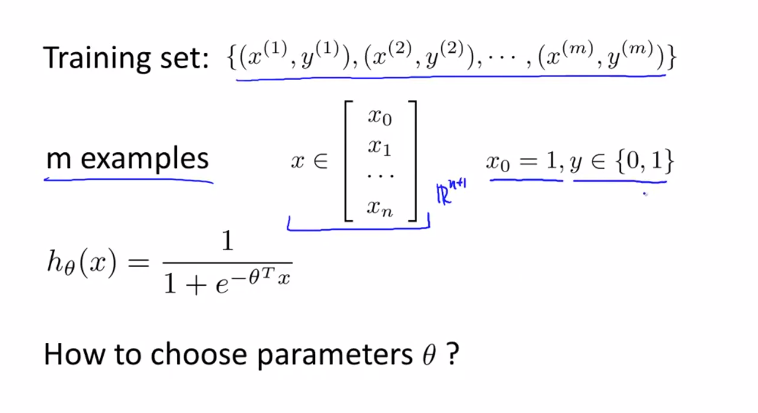
이번 강의에서는 로지스틱 회귀(Logistic regression) 를 위한 $ \theta $를 구하는 방법에 대해 알아봅니다.

선형 회귀 모델에서 사용한 비용 함수를 위첨자를 생략하고 간략하게 나타내면 다음과 같은 식을 얻을 수 있습니다.

$$ Cost(h _{\theta}(x), y) = \frac{1}{2}(h _{\theta}(x) - y)^{2} $$

로지스틱 회귀 문제를 다룰 때 $ h _{\theta}(x) = \frac{1}{1+e^{{\theta}^{T}x}} $ 로 비선형성을 가지게 됩니다. 여기에 비용 함수 $ J({\theta}) $를 구하면 Non-Convex(비볼록 함수) 모양을 가지게 됩니다.

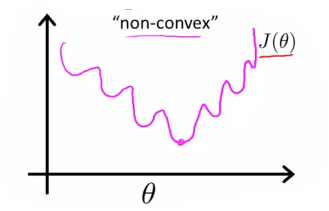
이러한 비볼록 함수의 경우 gradient descent를 적용해도 전체 함수의 최소값에 도달한다는 보장이 없습니다. 그렇기 때문에 우리는 로지스틱 회귀에서 사용할 비용 함수는 다음과 같습니다.

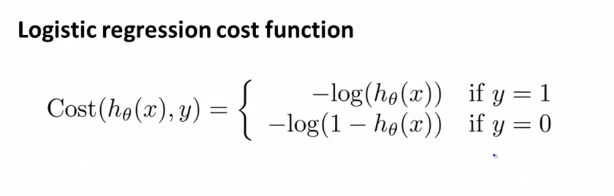
비용 함수는 y=0일때와 y=1일 때를 나타내고 있습니다. y=1일때의 함수를 그리면 다음과 같습니다.

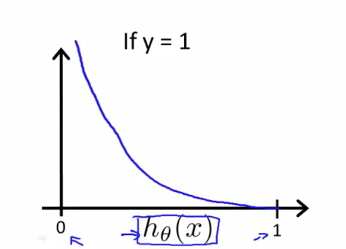
이 비용 함수의 특징을 보면 y=1 인 경우 h(x)=1 입니다. 다시말해 가설을 정확하게 예측한 경우 비용은 0이 됩니다. 하지만 h(x) 가 0에 가까워지면 비용은 무한대가 됩니다.

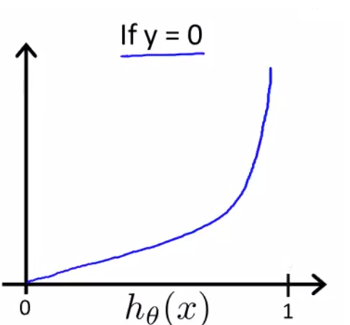
y=0 일때의 그래프를 확인하면 이러한 모양이 됩니다.

Simplified Cost Function and Gradient Descent

우리는 앞에서 y=0 또는 y=1 두가지 케이스로 나누져 있는 비용 함수에 대해 알아봤습니다. 이 두 줄의 식을 하나의 방정식으로 표현이 가능합니다.

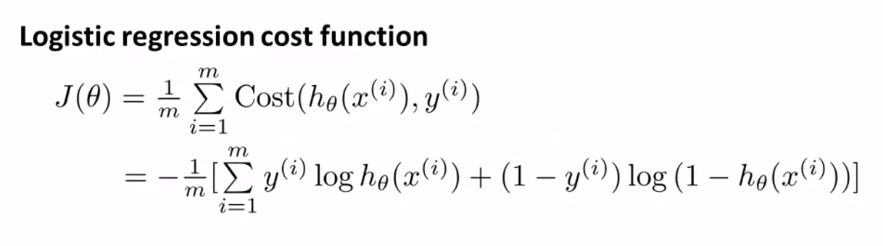
우리는 다른 비용 함수들을 선택할 수도 있지만 이 비용 함수는 최대우도 추정법(Maximum likelihood estimation)의 원리를 이용한 통계로부터 유도 되었고 $ =theta $를 구하는데 효율적이기 때문에 많이 사용됩니다.

Advanced Optimization

Gradient descent 만이 우리가 사용할 수 있는 유일한 알고리즘은 아닙니다. 다른 고급 최적화 알고리즘을 사용해 Gradient descent 를 사용하는 것보다 훨씬 빠르게 최적의 값을 구할 수 있습니다.

Gradient descent 외에도 위와 같은 Conjugate gradient, BFGS, L-BFGS 알고리즘이 있습니다. 이 알고리즘의 장점은 $ \alpha $(learning rate) 를 자동으로 선택해 줍니다. 단점으로는 gradient descent 보다 훨씬 복잡하다는 점 입니다. 그렇기 때문에 이러한 알고리즘의 경우 소프트웨어 라이브러리를 사용하는 것을 권장합니다.

Multiclass Classification : One-vs-all

결과값이 여러개로 분류되는 문제(Multiclass)의 예시로는 위와 같은 것들이 있습니다. 위의 예시중 email 분류를 보게되면 업무, 친구, 가족, 취미와 같이 ‘0’, ‘1’만으로는 표현할 수 없는 분류 문제가 있습니다.

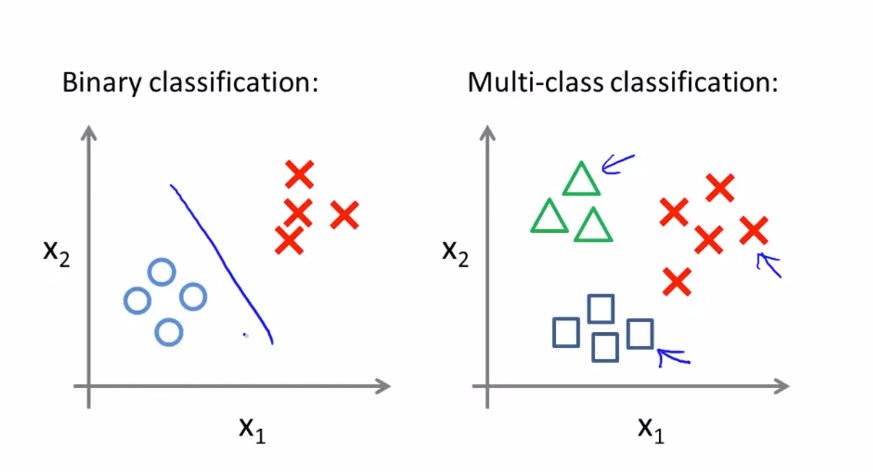
이전에 다뤘던 Binary classification 은 왼쪽 그림과 같이 2개의 class 로 나누어져 있지만 Multi-class classification 은 오른쪽 그림과 같이 2개 이상의 class 로 구성돼있습니다. 이와 같은 데이터 집합을 분류하는데에 One-vs-all 분류 알고리즘을 사용할 수 있습니다.

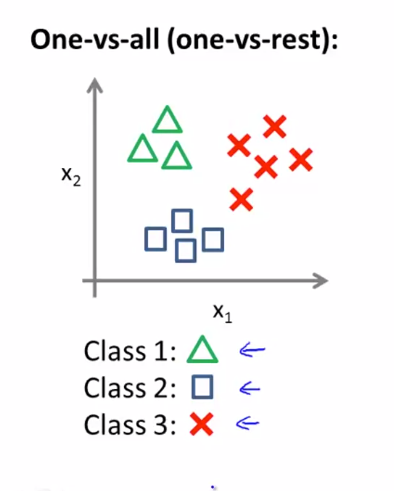
우리는 위 데이터를 세 가지로 나누어진 binary classification 문제로 바꿀 것입니다.

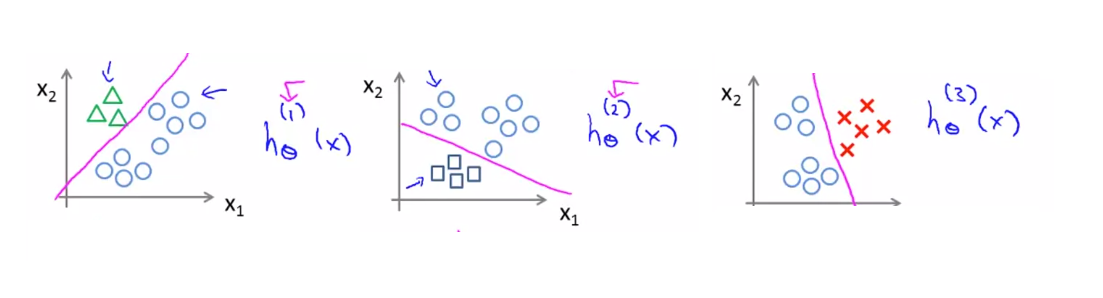
위의 그림과 같이 class1 에 대한 훈련, class2, class3 에 대한 훈련을 각각 진행해 class 각각의 경계선을 얻을 수 있습니다. 이제 새로운 입력값 x가 주어진다면 이 3가지의 h에 전부 돌려보고 최대값이 나온 클래스를 고르면 됩니다.