[Coursera][Muchine Learning] Neural Networks 인공 신경망
- 이 포스팅은 Andrew Ng 교수님의 Machine Learning 강의를 정리했습니다.
Motivations : Non-linear Hypotheses
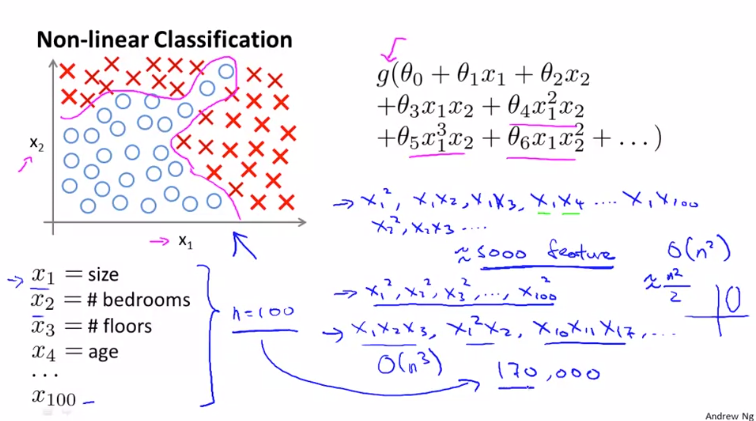
기존에 배운 선형 회귀와 로지스틱 회귀는 복잡한 데이터를 처리하는데에 한계가 있습니다. 위와 같이 오직 두개의 요소 $ x _{1} $, $ x _{2} $ 가 주어진 경우 수많은 다항식을 포함한 로지스틱 회귀를 적용할 수 있습니다. 하지만 요소가 많아진다면 어떨까요?
이전에 살펴본 주택 문제를 100가지의 요소를 가진 분류 문제로 살펴봅니다. 여기서 모든 2차항들을 사용한다면 우리는 5000개가 넘는 요소를 포함하게 됩니다. 그렇게 될 경우 계산하는데 시간이 많이 소요되고 과적합(overfitting) 문제가 생길 수 있습니다.
Computer vision을 살펴봅니다.
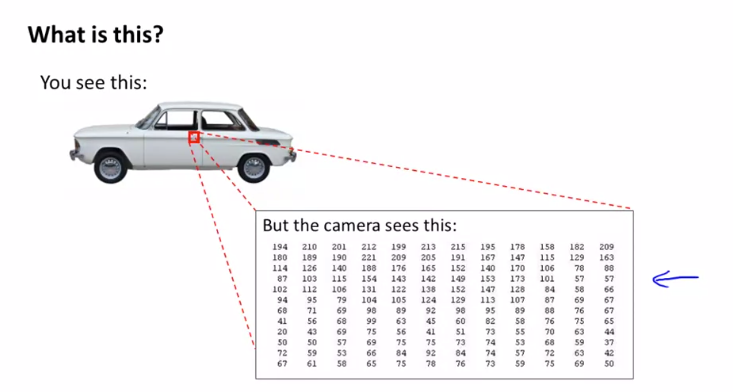
이미지의 작은 영역을 확대해서 보도록 합니다. 컴퓨터는 이 부분을 픽셀(Pixel) 값으로 이루어진 행렬로 바라보게 됩니다. Computer vision문제는 컴퓨터가 이러한 행렬을 보고 우리에게 자동차 문 손잡이를 나타낸다고 말해줘야 합니다.
구체적으로, 우리가 기계학습을 이용해 차량을 식별하기 위해서는 label training set 이 필요합니다. 즉, ‘자동차’, ‘차동차가 아님’ 이라고 표시된 아래와 같은 train set 을 준비해야합니다.

이제 비선형 가설을 사용하는 경우 대해 알아 봅시다.
다음과 같은 자동차 이미지에서 픽셀1, 2를 골라 그래프로 나타내면 아래와 같습니다.
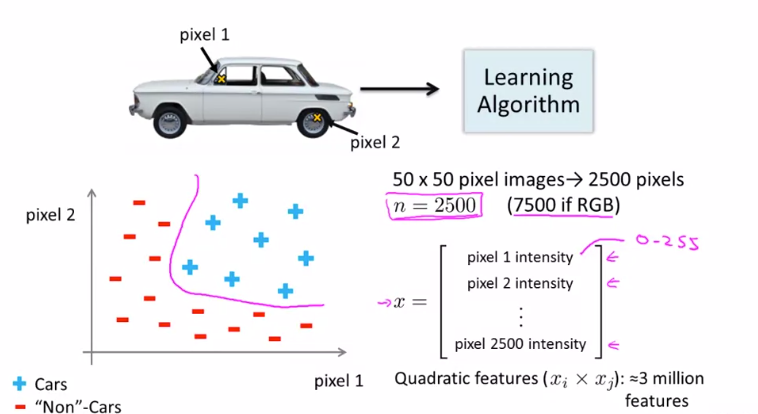
‘자동차’를 나타내는 ‘+’ , ‘자동차가 아님’ 을 나타내는 ‘-’ 를 사용해 표시합니다. 여기서 50x50 픽셀 이미지를 사용한다고 가정하면 우리는 2500개의 픽셀을 가지게 됩니다. 따라서 특징 공간의 차원 n 은 2500입니다. 여기서 모든 이차 요소를 포함하려고 하면 2500 픽셀이 약 300만개의 요소로 늘어나 많은 시간이 소요되게 됩니다.
Neural Networks : Model Representation I
인공 신경망(Neural Networks) 를 어떻게 표현하는지 알아봅니다. 인공 신경망은 뇌속의 뉴런이나 뉴런 연결망처럼 보이게 만들어졌습니다. 우선 뇌속의 단일 뉴런에 대해 살펴보겠습니다.
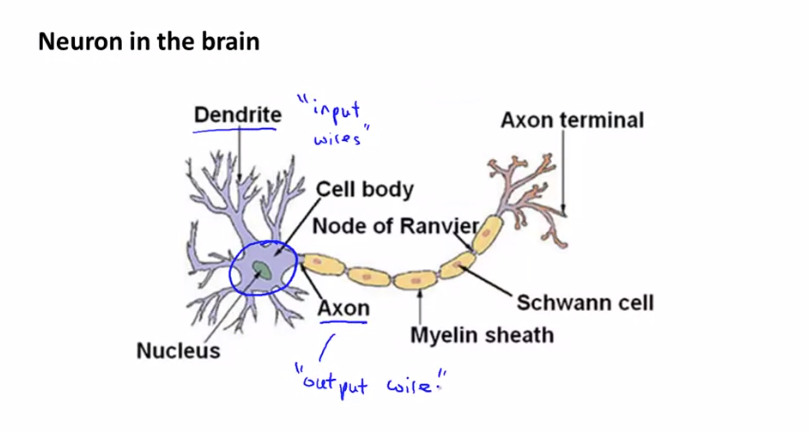
뉴런은 수상돌기(Dendrite)에서 입력을 받아 특정 계산을 수행하고 축삭돌기(Axon)을 통해 출력 값을 다른 노드나 뉴런으로 보냅니다.
뉴런이 동작하는 방식을 단순하게 표현한 모델을 살펴봅니다.
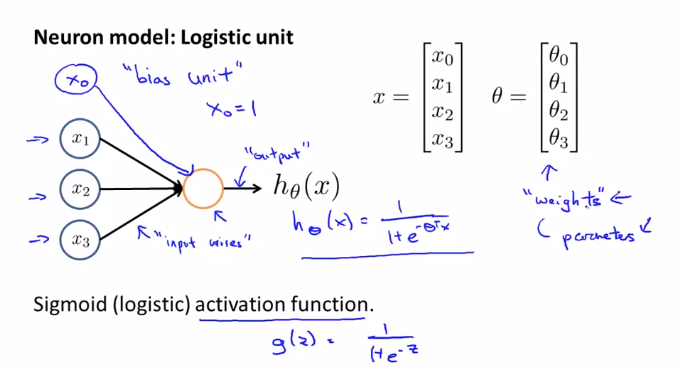
여기서 $ x _{0} $는 bias unit 또는 bias neuron 이라고 불리는데, 항상 1이여서 가독성을위해 생략하기도 합니다. 우리는 뉴런을 Sigmoid 인공 뉴런 또는 Logistic activation 함수 라고 부릅니다. 그래서 인공 신경망에서도 $ \frac{1}{{1}+e^{(-{\theta}^{T}x)}} $ (Sigmoid Function) 을 사용합니다. $ \theta $ 는 인공 신경망 용어로 모델의 가중치(Weights) 라고 표현하기도 합니다.
위의 모델은 하나의 뉴런을 나타낸 것입니다. 인공 신경망은 뉴런들이 여러개 연결된 것입니다.
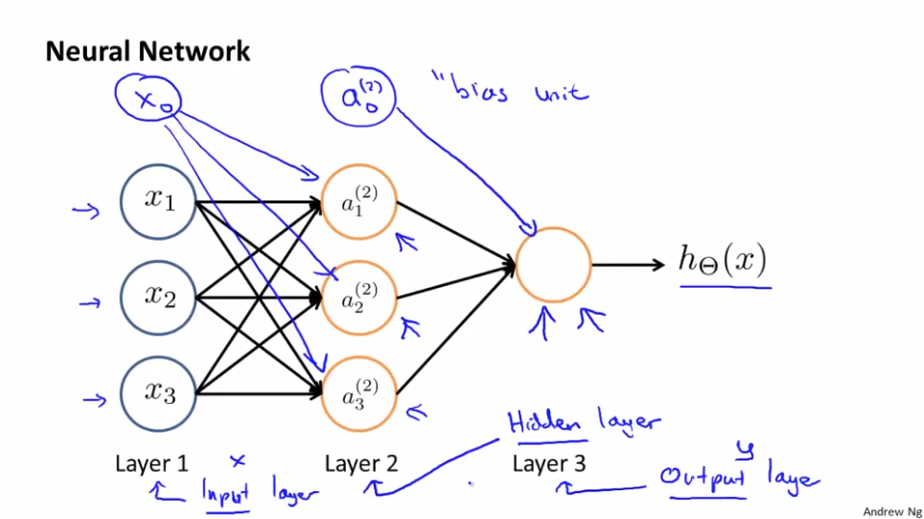
인공 신경망에서 첫 번째 Layer 를 Input Layer 라고 부르고 이곳에서 feature( $ x _{1} $, $ x _{2} $, $ x _{3} $) 를 입력 받습니다. 마지막 세 번째에 있는 Layer 는 Output Layer 라고 부르고 하나의 뉴런을 가지고 있기 때문에 가설을 계산한 최종 값을 출력합니다. 사이에 있는 Layer 는 Hidden Layer (이 Layer에 있는 값들은 training set 에서 볼 수 없기 때문에 Hidden이라는 말을 사용) 라고 부르는데 신경망은 여러개의 Hidden Layer 를 가질 수 있습니다.

신경망에서 $ a _{i}^{(j)} $ 는Layer j에 있는 unit ‘i’ 의 계산된 Output 값(activation)을 나타내기 위해 사용하며 $ \Theta^{(j)} $ 는 Layer j 에서 Layer j+1 로 매핑하는 함수를 조절하는 가중치(weights) 의 행렬 입니다.
위의 3개의 Input Layer와 3개의 Hidden Layer 를 가지는 신경망 다이어그램을 식으로 나타내면 다음과 같습니다.

인공 신경망은 함수 h를 정의하는 것인데, 함수 h는 x를 입력받아 y를 예측하는 함수입니다. 이 가설 함수 h는 파라미터 $ \Theta $ 에 의해 조절되고 $ \Theta $ 를 변화시키면 h 뿐만 아니라 x에서 y로 매핑하는 함수 또한 달라지게 됩니다.
Neural Networks : Model Representation II
Forward propagation : Vectorized implementation
실제로 계산을 효율적으로 수행하는 방법을 살펴봅니다.
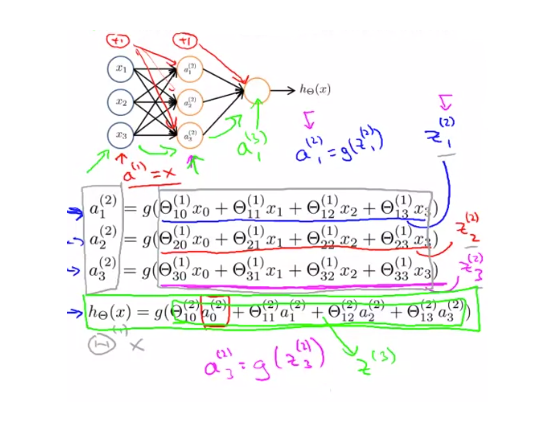
우리는 이전에 다음과 같이 표현할 수 있다는 것을 배웠습니다.
$$ a _{1}^{(2)} = g(z _{1}^{(2)}) $$
$$ a _{2}^{(2)} = g(z _{2}^{(2)}) $$
$$ a _{3}^{(2)} = g(z _{3}^{(2)}) $$
여기서 입력값들을 벡터로 표현할 수 있습니다.
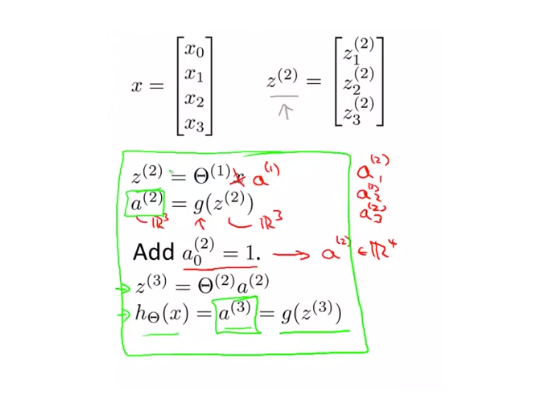
최정적으로 $ \Theta^{(j-1)} $ 은 하나의 행을 가지므로 single number 가 됩니다. 이런식으로 신경망에서 Input Layer 부터 Output Layer 까지 순서대로 이동하면서 x의 h를 계산하는 과정을 순방향 전파(Forward Propagation) 라고 합니다
Neural Network learning its own features
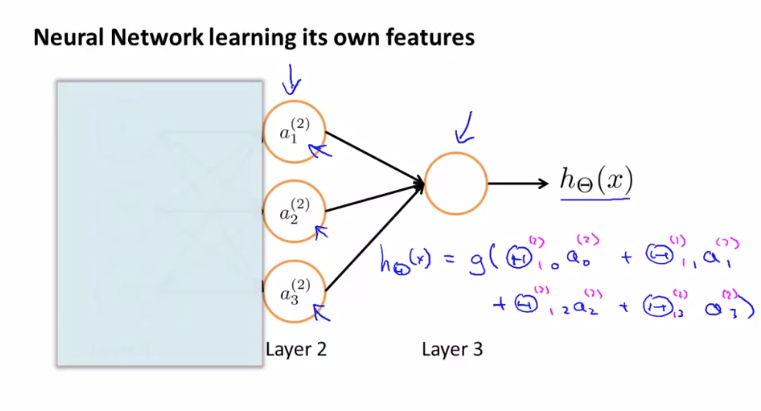
왼쪽 경로를 은폐한다고 가정하면 이 신경망이 하는 일은 로지스틱 회귀 분석처럼 보입니다. 로지스틱 회귀 분석에 공급되는 기능은 Hidden Layer 에 의해 계산 된 값입니다.
Applications : Examples and Intuitions I
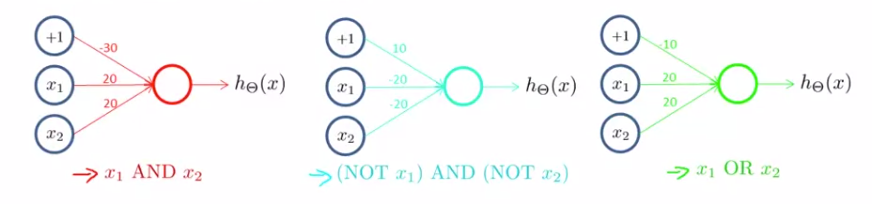
- simple example : AND
$ x _{1} $ 와 $ x _{2} $ 를 입력으로 받는 AND 논리 연산 예제를 살펴봅니다
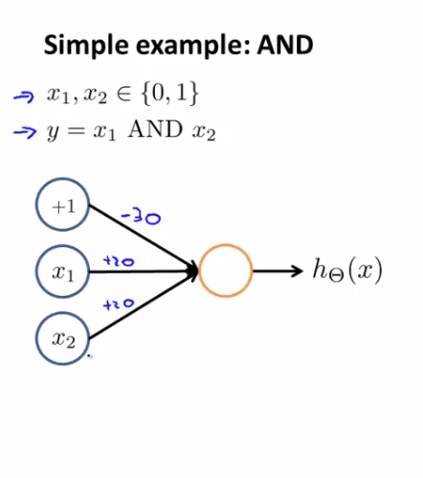
여기서 +1이 나타내는 것은 bias unit 입니다. 매개 변수에 -30, 20, 20을 순서대로 할당해 주게되면 다음과 같은 가설 함수를 얻을 수 있습니다.
$$ h _{\Theta}^{(x)} = g(-30 + 20x _{1} + 20x _{2}) $$
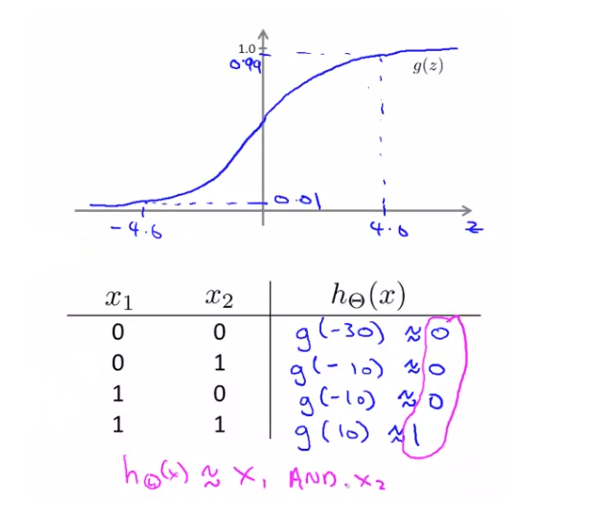
sigmoid 그래프와 카르노 맵을 통해 계산 과정을 살펴보면 $ x _{1} $ 와 $ x _{2} $ 가 모두 1일 때에만 1을 출력하는 것을 확인할 수 있습니다. 이는 AND 논리 연산을 나타내는 것을 알 수 있습니다.
- Example : OR function
OR 논리 연산 또한 비슷합니다.
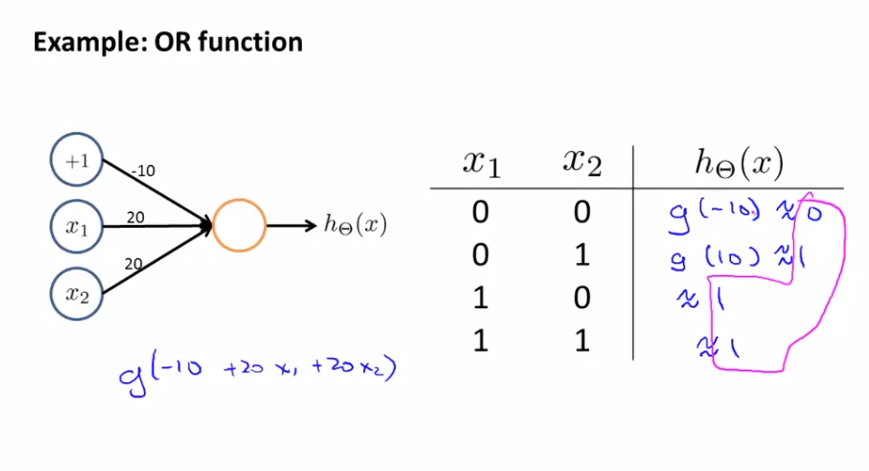
매개 변수 할당을 -10, 20, 20으로 한다면 OR 논리 연산을 확인할 수 있습니다.
Examples and Intuitions II
- Putting it together : $ x _{1} $ XNOR $ x _{2} $
앞서배운 AND 와 OR 논리 연산을 조합하여 XNOR 연산자를 만들 수 있습니다.
첫번째 Layer 와 두번째 Layer 에서 AND와 NOR를 조합해 사용하고 두번째 Layer 와 Output Layer 는 OR를 사용합니다.
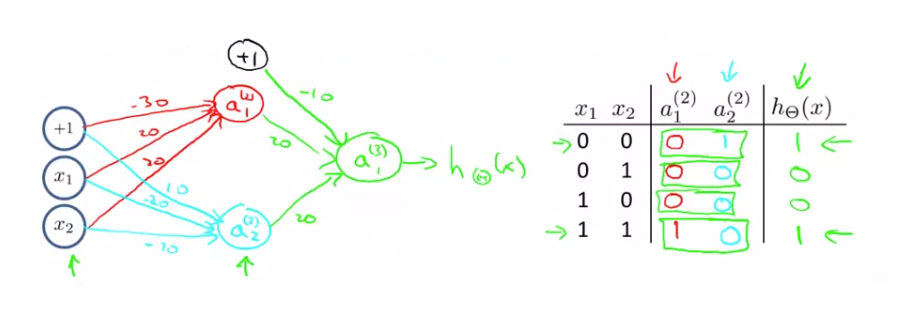
이 방법을 통해 Neural Network로 XNOR 연산자를 만들 수 있습니다.
Multiclass Classification
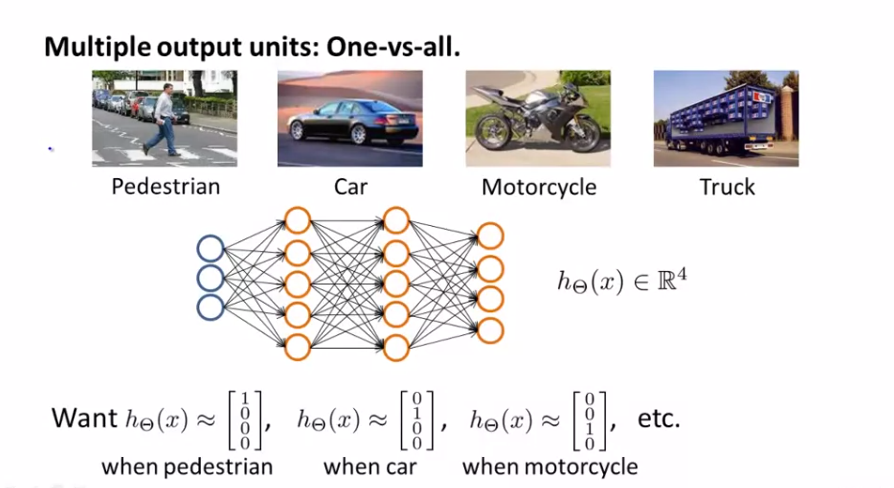
다중 분류(multiclass classification)를 신경망을 이용해 분류하기 위해서는 이전에 사용한 One-Vs-All 의 확장된 방법을 사용해야합니다. 위의 사진을 Pedestrian, Car, Motorcycle, Truck 으로 분류하기 위한 예제를 살펴봅니다. 이렇게 4종류로 분류하기 위해서는 Output Layer 에 4개의 Unit을 넣도록 구성하면 됩니다.
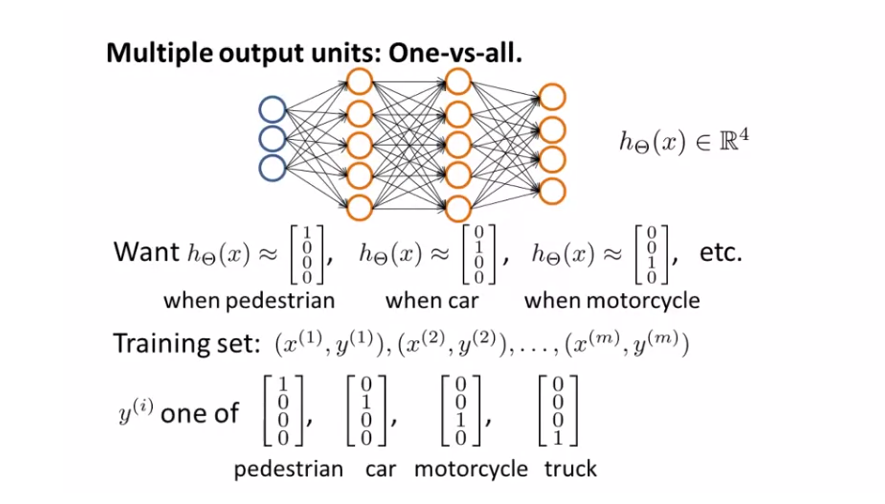
그렇게 되면 Output Layer 는 4차원 Vector 를 나타내게 됩니다.