• 이 포스팅은 Andrew Ng 교수님의 Machine Learning 강의를 정리했습니다.

Octave 설치

이 강의에서는 Octave 라는 수치해석용 오픈소스 프로그램을 사용합니다.

Octave 는 여기에서 받을 수 있습니다.

설치 후 실행한 모습 (강의에 사용한 버전과는 많이 달라진 모습)

Octave Tutorial

기본적인 연산과 행렬을 다루는 부분은 제외했습니다.

Vectorization

벡터화의 예시를 살펴봅니다.

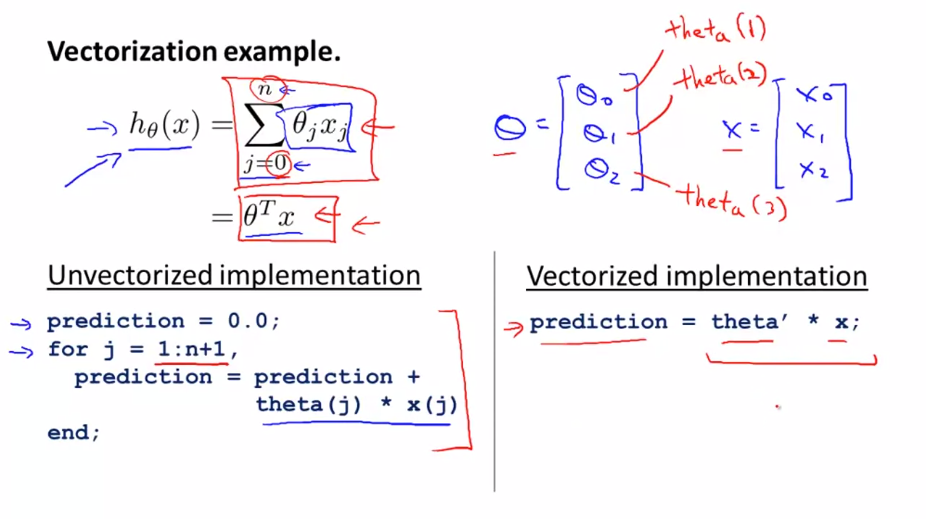
h(x) 를 계산하는데에 비 벡터화(Unvectorized) 방법과 벡터화(vectorized) 방법이 있습니다. 이를 Octave 코드로 구현하면 다음과 같습니다. 위 코드를 보면 비 벡터화 방법은 4줄의 코드로 표현되지만 벡터화는 한줄로 표현할 수 있습니다.

벡터화 문제는 Octave 뿐만 아니라 다른 프로그래밍 언어에도 적용됩니다. 다음은 C++ 언어 입니다.

C++ 에서 선형 대수 라이브러리를 사용하면 다음과 같이 간단하고 효육적인 코드를 작성할 수 있습니다.

이번에는 선형 회귀의 Gradient descent 예시로 알아보겠습니다.

우리는 J = 0, 1 ,2 등 모든 값에 대해 $ \theta _{j} $ 를 업데이트 해야합니다.

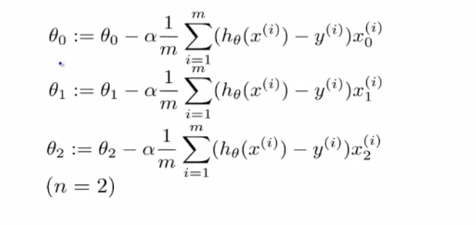
위의 식을 벡터화로 구현해내는 방법을 살펴보겠습니다.

시그마 부분을 $ \delta $를 사용해 간결하게 표현합니다.

$$ \theta := \theta - \alpha \delta $$

$ \theta $ 와 $ \delta $ 는 n+1 차원 벡터이고 $ \alpha $ 는 실수입니다.

$ \delta $를 벡터로 표현하면 다음과 같습니다.

$$ \delta = \begin{bmatrix} \delta _{0} \\ \delta _{1} \\ \delta _{2} \end{bmatrix}$$

여기서 $ \delta $ 의 시그마 부분 $ \sum _{i=1}^m (h _{\theta}(x^{(i)}) - y^{(i)})x^{(i)} $ 는

$$ (h _{\theta}(x^{(1)}) - y^{(1)})x^{(1)} \\ (h _{\theta}(x^{(2)}) - y^{(2)})x^{(2)} \\ (h _{\theta}(x^{(3)}) - y^{(3)})x^{(3)} $$

로 표현됩니다.

여기에 $ x^{(i)} $ 도

$$ x^{(i)} = \begin{bmatrix} x _0^{(i)} \\ x _1^{(i)} \\ x _2^{(i)} \end{bmatrix}$$

의 벡터입니다.

$ \delta $ 를 표현해보면 다음과 같이 나타 낼 수 있고

$$ \delta = \frac{1}{m}(x^{T}x - x^{T}y) $$

최종적으로 $ \theta $ 는

$$ \theta := \theta - \frac{\alpha}{m}(x^{T}x - x^{T}y) $$

로 나타낼 수 있습니다.