• 이 포스팅은 Andrew Ng 교수님의 Machine Learning 강의를 정리했습니다.

Regularization : The Problem of Overfitting

로지스틱 회귀(Logistic Regression)과 선형 회귀(Linear Regression) 알고리즘을 머신러닝 문제들에 적용시킬때, 과적합(overfitting) 문제에 빠져 성능이 안나올 수 있습니다.

계속 사용하던 집값 예측 문제를 통해 과적합(overfitting) 에 대해 알아봅니다.

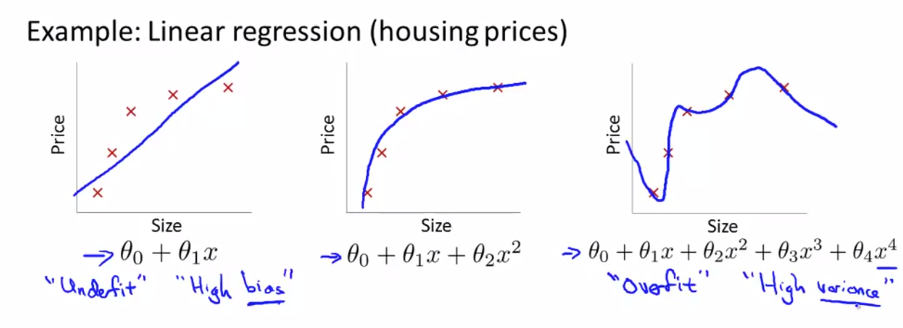
가장 왼쪽 그래프를 보면 데이터를 가로지르는 1차 함수를 그릴 수 있습니다. 하지만 집이 커질수록 집값이 완만하게 증가하는데에 비해 직선은 집이 커질수록 집값이 동일하게 커지는 것을 볼 수 있습니다. 그렇기 때문에 이 모델은 적합하지 않습니다. 이러한 문제를 과소적합(Underfitting) 또는 높은 편향(High bias)을 가지고 있다고 합니다.

가운데 있는 그래프는 2차 함수를 넣었습니다. 커브 모양으로 꽤 잘 맞는것을 볼 수 있습니다.

오른쪽 그래프는 좀 극단적인 예시인 4차 함수 그래프를 넣었습니다. 이 선은 데이터에는 잘 맞아 보이기 때문에 훈련용 데이터에 한해서는 좋은 성능을 낸다고 볼 수 있습니다. 하지만 새로운 데이터에 대한 일반화(Generalized)된 예측은 제대로 하지 못하는 문제가 발생합니다. 이러한 문제를 과적합(Overfitting) 또는 높은 분산(High variance)을 가지고 있다고 합니다.

여기까지는 선형 회귀에 대한 과적합 케이스였습니다. 과적합 문제는 로지스틱 회귀에서도 마찬가지 입니다. 로지스틱 회귀 예시를 확인해 보겠습니다.

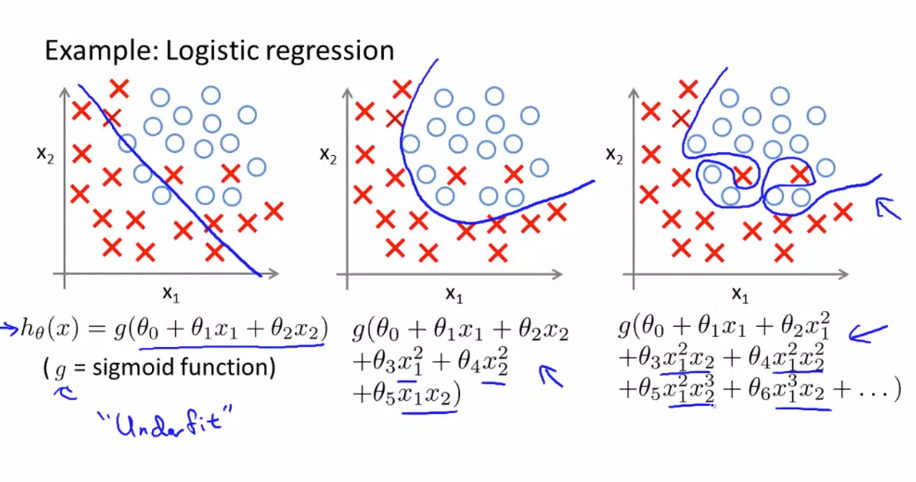
로지스틱 회귀도 선형 회귀와 마찬가지로 왼쪽부터 과소적합, 적합, 과적합입니다. 차원이 높아질수록 과적합의 우려가 있기 때문에 적당한 차원의 다항식을 선택해야합니다.

과적합 문제를 해결하기 위해서는 크게 두 가지 방법이 있습니다.

  1. 특성의 갯수를 줄인다.

특성들 중에 쓸만한 특성을 선별해 쓸만하지 않은 특성을 제거해 특성의 수를 줄이는 것이 과적합 문제를 해결할 방법으로 이용될 수 있습니다. 하지만 이 방법의 단점으로는 몇 가지 특성을 버리면서 문제에 포함된 정보를 같이 버리게 된다는 것입니다.

  1. 정규화(Regularization)

모든 특성을 남기되 각각의 특성이 가지는 영향 규모를 줄이는 것입니다. ($ \theta$ 값이 미치는 영향 감소)

Regularization : Cost Function

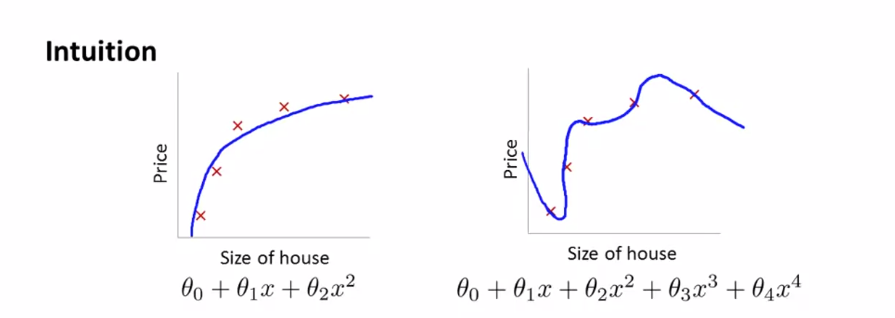
위의 내용에서 왼쪽 그래프(2차 함수)는 적합하고 오른쪽 그래프(높은 차수의 다항식)는 과적합이라고 설명했습니다.

위와 같은 높은 차수의 다항식에서 $ x^{3} $와 $ x^{4} $ 가 1000으로 큰 수를 가지고 있다고 하면 우리는 $ \theta _{3} $, $ \theta _{4} $ 를 0에 가깝게 만들어 4차함수를 2차 함수와 거의 같아지게 만들 수 있습니다.

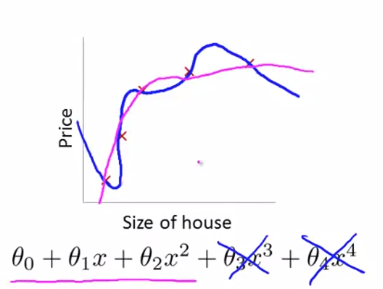
$ \theta _{3} $, $ \theta _{4} $를 0에 가깝게 만들어 제거하는 것처럼 만들게 된다면 훨씬 더 나은 가설을 얻을 수 있습니다.

이러한 방법으로 모든 매개 변수에 적용하면 가설 함수를 더 단순화해 과적합 문제가 발생할 가능성을 줄일 수 있습니다. 왜 모든 $ \theta $ 값에 대해 최소화를 해야하는지 이해가 잘 되지 않겠지만 직접 구현해보기 전까지는 설명으로 이해하기 어렵습니다.

다음 주택 가격 예측 예시를 보겠습니다.

주택 가격 예측 feature 로 $ x _{1} $은 크기, $ x _{2} $는 침실의 수, $ x _{3} $은 층의 수 등등 100가지의 특징이 있을 수 있습니다. 우리는 이 특징 중 어떤 값을 선택해 줄여야 하는지 미리 알지 못합니다. 그렇기 때문에 정규화를 사용할 것입니다.

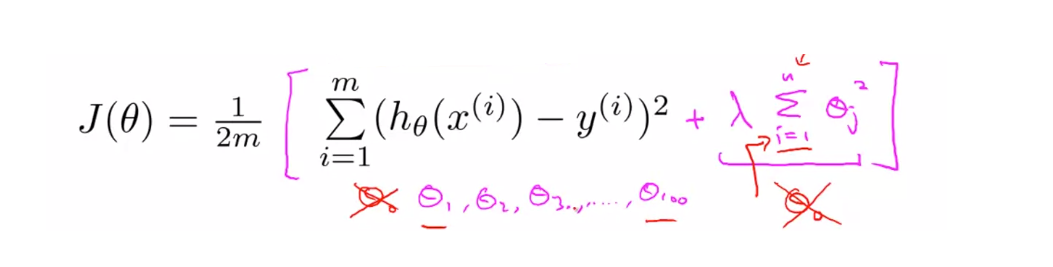
i=1 부터 시작하기 때문에 $ \theta _{0} $은 포함하지 않습니다. $ \theta _{0} $ 을 포함하지 않아도 지장이 별로 없습니다.

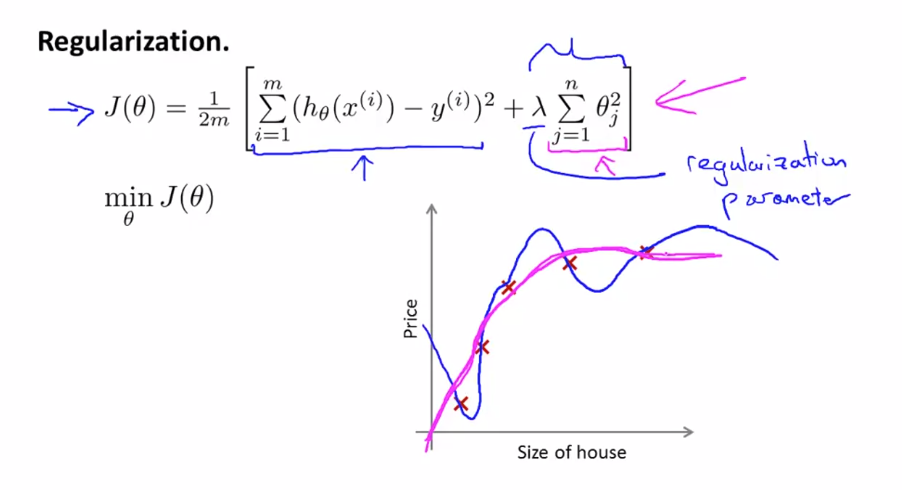
비용 함수에 붙은 $ \lambda \sum_ {j=1}^n \theta _{j}^2 $ 는정규화를 위한 수식이고 $ \lambda $는 정규화 매개 변수입니다. 정규화를 통해 기존의 굴곡이 많은 그래프를 좀더 원만하게 바꾸어 과적합을 방지할 수 있습니다.

만약 정규화 매개 변수 $ \lambda $ 가 매우 큰 값을 가지게 되면 $ \theta _{0} $을 제외하고 모두 0에 가까워 질 것입니다. 그렇게 된다면 $ h _{\theta}(x) = \theta _{0} $ 인 수평 직선을 얻을 수 있고 훈련 세트에 잘 맞지 않게됩니다.

Regularized Linear Regression

  • Gradient descent

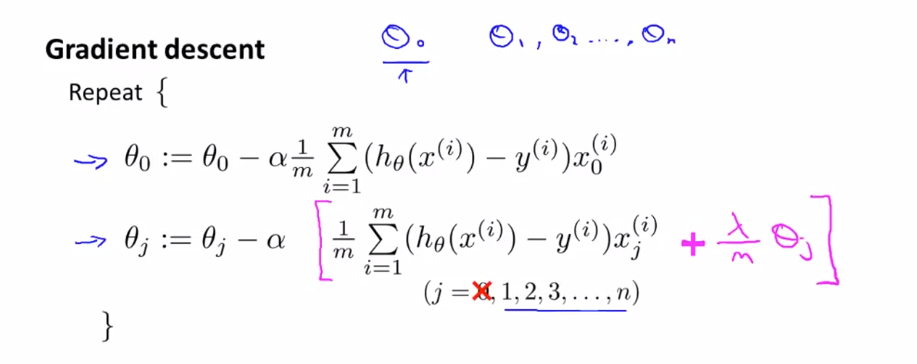
우리는 이 정규화 된 비용 함수 $ J(\theta) $를 최소화하는 $ \theta $를 찾을 것입니다. 이전에는 정규화 식이 없는 비용 함수에 gradient descent 를 사용했습니다. 이를 유사하게 사용하면 됩니다.

$ \theta _{0} $ 는 처벌하지 않기 때문에 따로 처리해줘야 합니다.

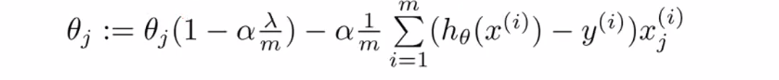
여기서 $ {1} - \alpha \frac {\lambda}{m} < {1} $ 이기 때문에 gradient descent 가 진행될 수록 $ \theta _{j} $ 는 감소하는 효과를 가지게됩니다.

  • Normal equation

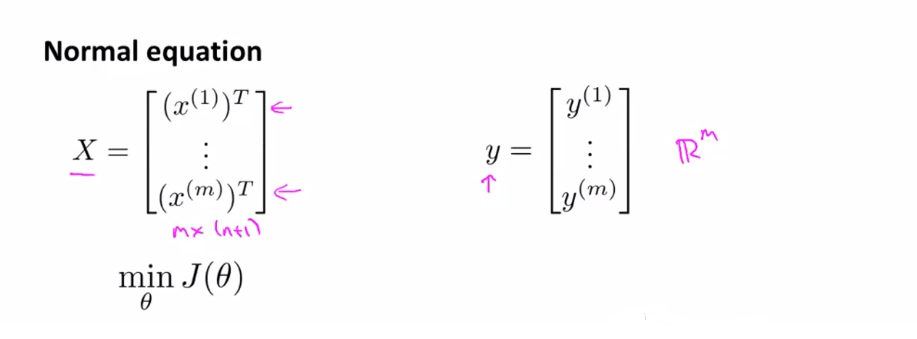
X는 (n+1) 차원 행렬, y는 m 차원 벡터입니다. 정규화 된 Normal equation을 보면 다음과 같습니다.

$$ \theta = (X^{T}X + \lambda \begin{bmatrix} 0 & 0 & 0 & … &0 \\ 0 & 1 & 0 & … &0 \\ 0 & 0 & 1 & … &0 \\ … & … & … & … &0 \\ 0 & 0 & 0 & … & 1 \end{bmatrix})^{-1}X^{T}y $$

여기서 $ \lambda $ 에 곱해진 행렬은 (n+1) X (n+1) 차원 행렬입니다.

비 가역성(Non-invertibility) 문제를 살펴봅니다.

$ m \leq n $ 일 때, $ X^{T}X $ 는 역행렬이 존재하지 않을 수 있습니다. 하지만 정규화를 사용하면 이러한 비 가역성 문제를 처리할 수 있습니다.

Regularized Logistic Regression

로지스틱 회귀 분석의 경우 gradient descent 와 Advanced Optimization 를 사용해 비용함수 $ J(\theta) $ 를 최적화하는 방법에 대해 배웠습니다.

로지스틱 회귀에서 위의 비용 함수는 과적합을 보였습니다. 여기에 정규화를 사용하기 위해서 $ \frac {\lambda}{2m} \sum _{j=1}^{n} \theta _{j}^{2} $ 를 기존 비용함수에 더해줍니다.

최종적으로 비용함수는 다음과 같습니다.

$$ J(\theta) = -[\frac {1}{m} \sum _{i=1}^{m}y^{(i)}log h _{\theta}(x^{(i)}) + (1 - y^{(i)}) log(1 - h _{\theta}(x^{(i)}))] $$

  • Gradient descent

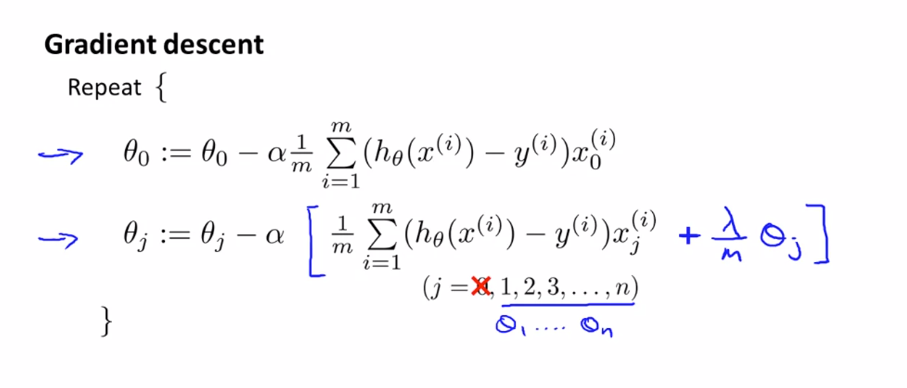
로지스틱 회귀의 정규화 된 gradient descent를 보면 정규화 된 선형 회귀와 동일해 보입니다. 하지만 여기에서 가설 함수는 $ h _{\theta}(x) = \frac {1}{1 + e^{-{\theta}^{T}x}} $ 이기 때문에 다르게 동작합니다.

  • Advanced Optimization

비용 함수 $ J(\theta) $ 를 계산하는 코드를 작성할 때, 끝에 $ \frac {\lambda}{2m} \sum _{j=1}^{n} \theta _{j}^{2} $ 를 포함시켜야 합니다. 위와 같은 과정을 거친 매개 변수는 정규화를 사용한 로지스틱 회귀 분석에 해당하는 매개 변수가 될 것입니다.