• 이 포스팅은 Andrew Ng 교수님의 Machine Learning 강의를 정리했습니다.

Implementation Note : Unrolling Parameters

Parameter $ \Theta $ 는 더이상 vector가 아니고 행렬을 나타냅니다. 이에 Octave에 사용하기 위해 Unroll과정이 필요합니다.

10 단위의 Input Layer, 10 단위의 Hidden Layer, 1단위의 Output Layer 신명망으로 살펴봅니다.

모든 요소를 긴 vector로 만듭니다. Theta1은 10x11 , Theta2 는 10x11, Theta3 는 1x 11 행렬을 얻을 수 있습니다.

위와 같이 비용함수를 구하는 함수를 구현할 수 있습니다.

Gradient Checking

gradient checking은 역전파를 진행하는데 나타나는 버그를 확인하고 거의 모든 문제를 제거하는 방법으로 항상 사용됩니다.

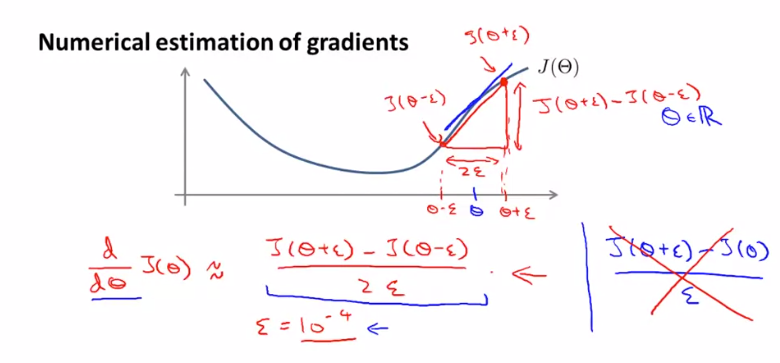
$ J({\Theta}) $ 가 주어지고 어떤 실수 값 $ \Theta $ 를 가지고 있다고 가정합니다.

이 $ \Theta $ 에서 $ \epsilon $ 만큼 떨어진 양쪽 지점에서의 기울기를 구하면 $ J({\Theta}) $ 의 미분계수를 추정할 수 있습니다. 여기서 $ \epsilon $ 이 작을수록 $ \Theta $ 의 기울기와 비슷해 집니다. 여기서 $ \epsilon = {10}^{-4} $ 를 사용합니다.

이를 Octave로 구현하면 다음과 같습니다.

gradApprox = (J(theta + EPSILON) - J(theta - EPSILON)) / (2*EPSILON)

Vector $ \theta $ 에 적용하면 다음과 같습니다.

Octave로 구현하면 다음과 같습니다.

for i = 1:n,
	thetaPlus = theta;
	thetaPlus(i) = thetaPlus(i) + EPSILON;
	thetaMinus = theta;
	thetaMinus = thetaMinus(i) - EPSILON;
	gradApprox(i) = (J(thetaPlus) - J(thetaMinus)) / (2*EPSILON);
end;

여기서 gradient check 로 얻은 gradApprox(i) 와 역전파로 계산된 DVec가 같은지 확인하면 됩니다.

Check that $ gradApprox \approx DVec $

정리하자면 gradient check 로 gradApprox(i)를 계산하고 역전파로 DVec를 계산해 두 vector가 유사한지 확인한 후 gradient check 의 사용을 중지한 후 계속해서 훈련을 진행합니다. 그렇지 않으면 실행이 매우 느려질 수 있습니다.

Random Initialization

경사 하강법(gradient descent) 또는 고급 최적화(advanced optimization) 알고리즘에 대한 초기값을 선택해야 합니다. 기존 로지스틱 회귀를 사용할 때는 $ \Theta $ 를 0으로 초기화 했을 때 잘 작동했지만 신경망에서는 작동하지 않습니다.

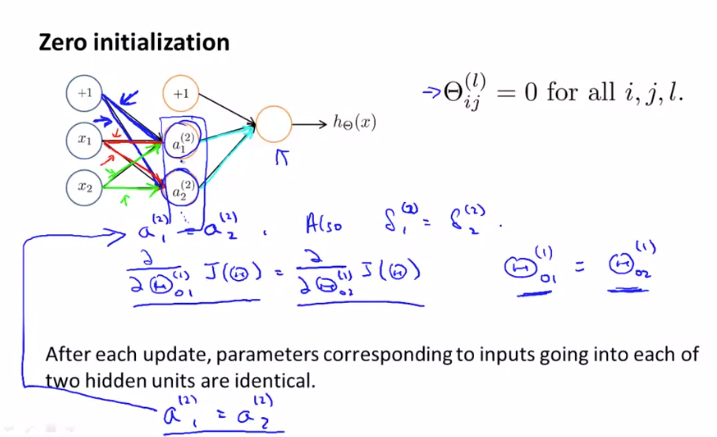
위와 같은 신경망에서 모든 매개 변수를 0으로 초기화 했다고 가정하고 진행하면 같은 Layer 에서 나온 $ \Theta $ 의 값들은 같은 값을 가지게 됩니다. $ \delta $ 또한 마찬가지로 같은 값을 가지게됩니다.

이러한 문제가 생기기 때문에 Random Initialization 을 사용해 parameter 를 초기화 합니다.

우리는 $ \Theta $ 의 각 값을 $ - \epsilon $ 과 $ \epsilon $ 사이의 난수로 초기화 해야합니다. 이때의 $ \epsilon $ 은 gradient checking 과 무관합니다.

이를 Octave 로 나타내면 다음과 같습니다.

Theta1 = rand(10,11) * (2 * INIT_EPSILON) - INIT_EPSILON;
Theta2 = rand(1,11) * (2 * INIT_EPSILON) - INIT_EPSILON;

Putting It Together

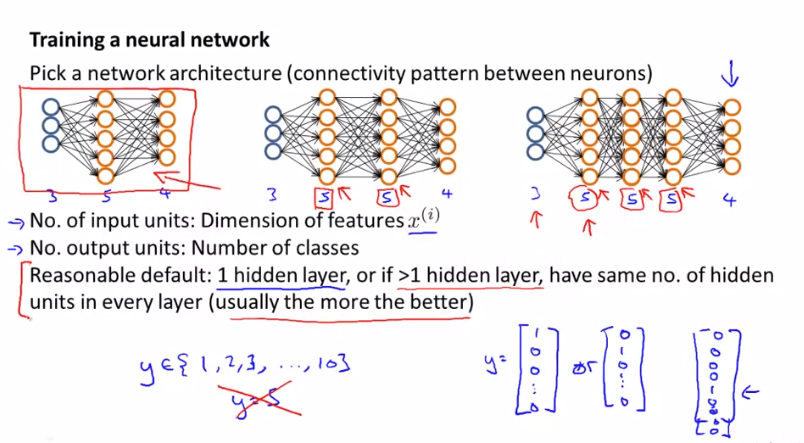
신경망을 훈련할 때 가장 먼저 해야 할 일은 Network Architecture를 선택해야 하는 것입니다. 즉, Input Layer의 unit 개수, Hidden Layer의 수, Output Layer의 unit 개수를 결정해야 합니다. 여기서 Hidden Layer 는 1개 이상도 가능하며, 각 Hidden Layer의 unit 개수는 동일하게 설정하는 것이 보통 좋은 성능을 가집니다. 계산비용이 많이들 수 있지만 Hidden Layer의 unit의 개수는 많을 수록 좋습니다.(대신 연산속도가 느려질 수 있음)

신경망의 training 순서는 위와 같습니다.

$ \Theta $ 를 초기화 하고 training set 학습을 진행하면서 순전파와 역전파를 수행합니다. 그리고 gradient checking을 통해 역전파의 오류를 확인하며 최적의 값이 되는 $ J({\Theta}) $ 를 구하면 됩니다.

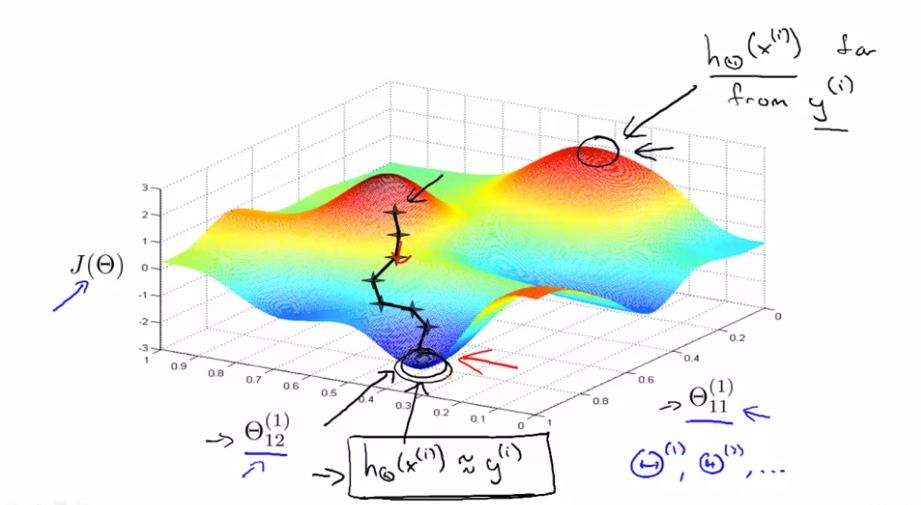
위 이미지는 2개의 Parameter를 갖는 신경망의 gradient descent 알고리즘의 수행을 보여주고 있습니다. 최저점에서 $ h _{\Theta}(x^{(i)}) $ 는 실제값 $ y^{(i)} $ 에 가장 근접한 것을 알 수 있습니다. 여기서 역전파는 gradient descent의 방향을 설정해주는 역할을 합니다.