경사 하강법 (Gradient Descent)

경사하강법(Gradient Descent) 는 머신러닝이나 딥러닝 모델에서 최적화를 위해 사용하는 방법 중 하나입니다. 말 그대로 Gradient(기울기)를 이용해 함수의 최대값 및 최소값을 사용하는데 사용됩니다. 그러면 경사하강법을 이해하기 위해 미분부터 알아보겠습니다.

미분 (Differentiation)

미분은 변수의 움직임에 따른 함수값의 변화를 측정하는데 사용되는 도구로 최적화에서 제일 많이 사용되는 기법입니다. 공식을 보면 다음과 같이 변화율의 극한으로 정의됩니다.

$$ f’(x) = \lim_{h \rightarrow 0} \frac{f(x+h) - f(x)}{h} $$

수식적으로 확인하게 되면 다음과 같습니다.

$$ f(x) = x^{2} + 2x + 3 $$

$$ \downarrow $$

$$ f’(x) = 2x + 2 $$

미분은 함수 f 의 주어진점 (x,f(x)) 에서의 접선의 기울기를 나타냅니다. 좀 더 직관적으로 알아볼 수 있게 그림으로 확인해봅니다.

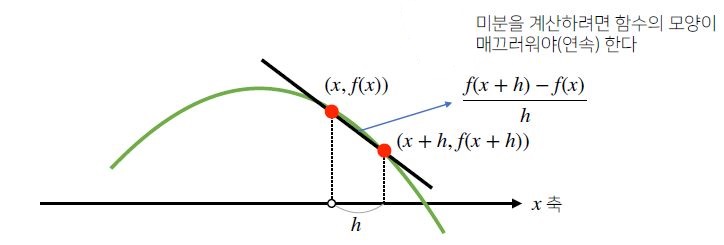
위와 같은 두 점의 기울기에서 h를 0에 가까이 보내게 되면

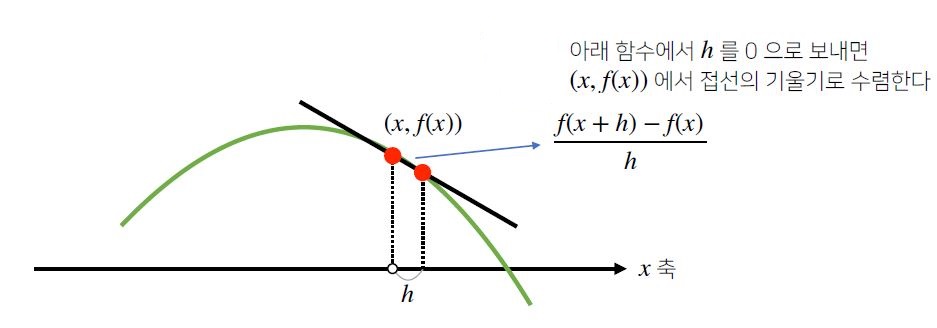
접선의 기울기로 수렴하게 됩니다.

Gradient Descent / Ascent

함수 f의 (x, f(x)) 에서 접선의 기울기를 알게 되면 어느 방향으로 움직여야 함수값이 증가하거나 감소하는지 알 수 있습니다.

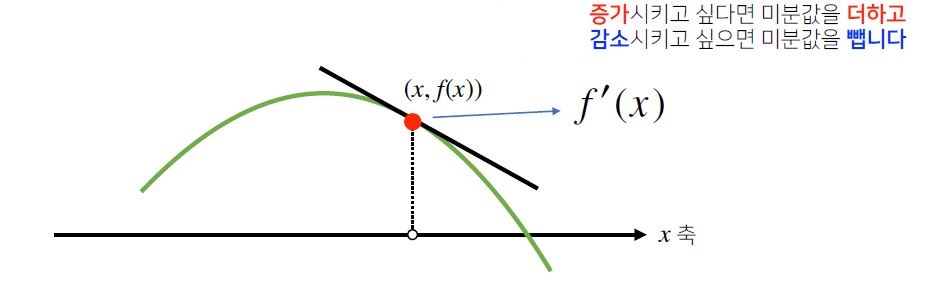
미분값을 더해 함수의 극대값의 위치를 구하는 방법은 다음과 같고 이것을 **경사상승법(Gradient Asecent)**라고 합니다.

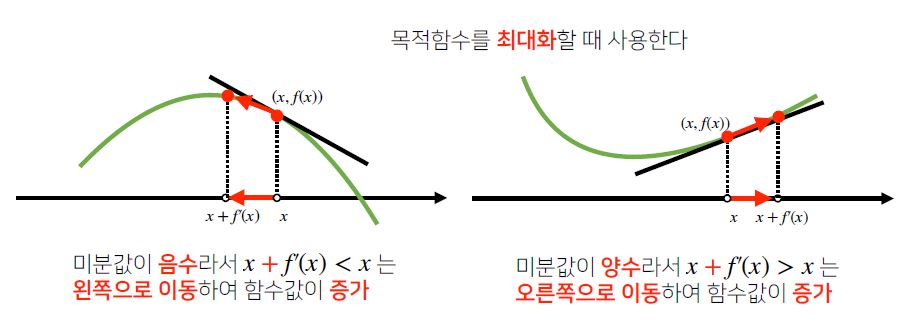
반대로 미분값을 빼면서 함수의 극소값의 위치를 구하는 방법을 **경사하강법(Gradient Descent)**라고 합니다.

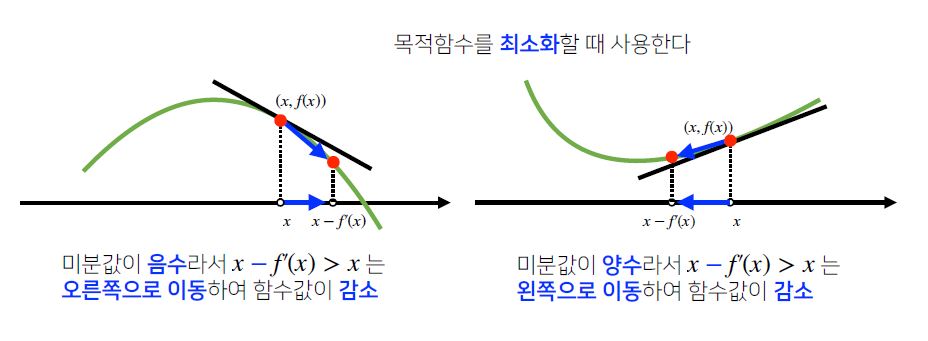
경사상승법과 경사하강법은 **극값(미분값이 0이 되는 지점)**에서 더 이상 업데이트가 되지 않고 자동으로 종료됩니다.

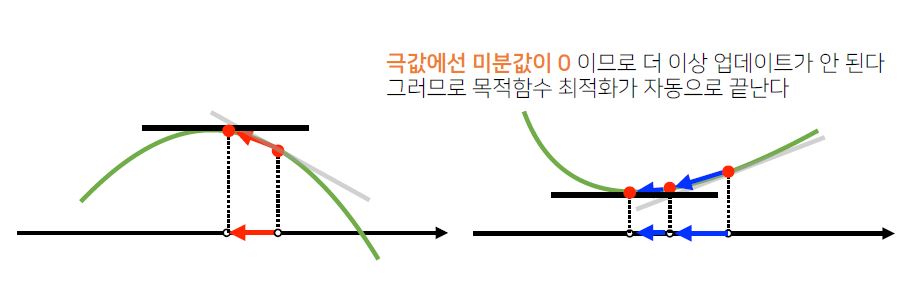
경사상승법 및 경사하강법은 2차원 뿐만아니라 n차원에서도 사용이 가능합니다.